O Capítulo 7 já foi contemplado em
https://seclusao.art.blog/2019/12/26/historia-da-matematica-uma-visao-critica-desfazendo-mitos-e-lendas-tatiana-roque-2012-capitulo-7-o-seculo-xix-inventa-a-matematica-pura-ou-a-era-do/. A seguir, citações dos demais.
Anexo: A história da matemática e sua própria história
“Quase todos esses autores escreveram seus textos mais importantes antes dos anos 1970, logo, sua visão sobre a história da matemática já pode ser considerada ultrapassada. Não queremos desmerecer o trabalho desses pioneiros, que ajudaram a fundar a história da matemática como campo de pesquisa e motivaram o interesse de inúmeros jovens por essa área. A intenção aqui é ressaltar que suas obras continuam a ser citadas sem uma visão crítica, ainda que inúmeros trabalhos históricos, nas últimas décadas, tenham desmentido e questionado grande parte das afirmações nelas reproduzidas. Até esse momento, os livros de história da matemática eram escritos, principalmente, por matemáticos e professores. A década de 1970 marcou uma virada na historiografia, pois a profissão de <historiador da matemática> começou a existir. Tal mudança se deu primeiramente nos Estados Unidos, mas também em outros países, cuja produção histórica anterior também era intensa, apesar de menos conhecida no Brasil.
A história da matemática teve um período de grande atividade na Europa entre as últimas décadas do século XIX e a Primeira Guerra Mundial. Um exemplo é a obra monumental do matemático alemão Moritz Cantor, Vorlesungen über Geschichte der Mathematik (Preleções sobre a história da matemática), publicada em 4 volumes entre 1880 e 1908 (este último volume com colaboradores), cobrindo um longo período: dos tempos antigos até 1200; de 1200 a 1668; de 1668 a 1758; e de 1759 a 1799. Outra iniciativa colossal foi a organização da Encyklopädie der mathematischen Wissenschaften (Enciclopédia das ciências matemáticas), coordenada por Felix Klein, que pretendia servir de fonte para uma visão geral sobre a área naquele momento, mas também sobre sua pré-história. O período foi marcado ainda por inúmeras edições de trabalhos originais de matemáticos renomados do passado, como as traduções dos textos gregos feitas por J.L. Heiberg (para o alemão), T.L. Heath (para o inglês) e P. Tannery (para o francês). Não é difícil imaginar que o período entre-guerras tenha interrompido essa intensa produção européia relacionada à história da matemática, um campo de pesquisas então incipiente. Depois da Segunda Guerra, houve trabalhos pontuais, como os de Otto Neugebauer, que, a partir de 1929, passou a liderar um grupo de historiadores sobre as matemáticas antiga e árabe. Estudos sobre outros períodos da história eram escassos, em parte devido ao predomínio da visão positivista em filosofia, mas também em outras áreas, o que pode ter influenciado os matemáticos e outros pesquisadores a pensarem que a <história era bobagem>.”
“1960 (…) Esse é um ano importante, pois marca a fundação de uma das revistas mais conhecidas até hoje dedicada especificamente ao tema: Archive for History of Exact Sciences. Apesar de esse periódico também ter divulgado, desde seus primeiros números, artigos de história da matemática, o movimento para reconhecer a história da ciência como área de pesquisa não foi acompanhado, de imediato, por um esforço similar para institucionalizar a história da matemática.”
“É curioso constatar que Uma história da matemática, livro escrito por Florian Cajori nas primeiras décadas do século XX, tenha sido traduzido para o português em 2007. Apesar de poder interessar à história da história da matemática, essa obra é bastante desatualizada.”
“Para combater o eurocentrismo, não nos parece profícuo tentar mostrar que o que os europeus descobriram já estava presente em outras culturas. Lançar-se em uma busca desenfreada pelas raízes não-européias da matemática pode levar alguns autores a exagerar para o outro lado, caso do best-seller de G.G. Joseph, Crest of the Peacock: Non-European Roots of Mathematics, publicado em 1991, em Londres, pela I.B. Taurus.”
“Sabetai Unguru, romeno que estudou filosofia e história da matemática em Israel e nos EUA, publicou em 1975 o polêmico artigo On the need to rewrite the history of mathematics, dirigindo forte crítica às histórias da matemática grega mais reconhecidas naquele momento, entre as quais se incluíam as de Neugebauer e de B.L. van der Waerden. Nesse artigo, os antigos historiadores da matemática grega são desqualificados como <matemáticos> e suas teses são apontadas como anacrônicas, marcadas por reconstruções racionais dos conteúdos com base na diferença entre necessidade lógica e necessidade histórica. Tal polêmica foi crucial para a definição da personalidade da história da matemática, contrastando interpretações conceituais, baseadas em uma imagem moderna da matemática, com estudos históricos que levavam em conta o contexto cultural.”
“Os trabalhos inovadores de Jöran Friberg, Jens Høyrup e Eleanor Robson, nos anos 80 e 90, transformaram de modo irreversível a imagem da matemática mesopotâmica, antes estudada por meio de reconstruções anacrônicas. A mesma revolução não aconteceu na história que aborda períodos mais recentes. O estudo da matemática na Idade Média e no Renascimento recebeu a influência dessas transformações no modo de fazer história, incluindo análises mais contextualizadas sobre o desenvolvimento geral da ciência, bem como da visão sobre a ciência na época. Mas a história da matemática moderna, que reconhecemos como mais próxima da nossa, está apenas começando a ser reescrita.”
“Um livro geral de história da matemática que pretende levar em conta essas novas pesquisas, cobrindo inclusive épocas mais recentes, é A History of Mathematics: an Introduction, publicado por V. Katz em 1993 e traduzido para o português como História da matemática. Trata-se de uma fonte confiável que, no entanto, devido à sua extensão, apresenta alguns temas de forma bastante resumida.”
“Ainda que o significado de noções como generalidade, universalidade e demonstração tenha mudado ao longo da história, o trabalho matemático foi executado, em diferentes momentos, como uma atividade demonstrativa, almejando produzir resultados segundo regras próprias a uma época dada. Os processos de abstração, bem como as manipulações simbólicas por meio das quais eles se manifestam, possuem uma história e foram traços característicos da prática matemática – sobretudo em épocas mais recentes – e, como tais, precisam ser analisados de perto.”
CAPÍTULO 1. Matemáticas na Mesopotâmia e no antigo Egito
“Como nosso objetivo é relacionar a história dos números com a história de seus registros, é preciso abordar o nascimento da escrita, que data aproximadamente do quarto milênio antes da Era Comum. Os primeiros registros que podem ser concebidos como um tipo de escrita são provenientes da Baixa Mesopotâmia, onde atualmente se situa o Iraque. O surgimento da escrita e o da matemática nessa região estão intimamente relacionados.”
“Em seguida, a região foi dominada por um império cujo centro administrativo era a cidade da Babilônia, habitada pelos semitas, que criaram o Primeiro Império Babilônico. Os semitas são conhecidos como <antigos babilônios>, e não se confundem com os fundadores do Segundo Império Babilônico, denominados <neobabilônios>. Data do período babilônico antigo (2000-1600 a.E.C.) a maioria dos tabletes de argila mencionados na história da matemática.
babilônicos (judeus) x mesopotâmicos (babilônios!)
“Por exemplo, o tablete YBC 7289 diz respeito ao tablete catalogado sob o número 7289 da coleção da Universidade Yale (Yale Babilonian Collection). Outras coleções são: AO (Antiquités Orientales, do Museu do Louvre); BM (British Museum); NBC (Nies Babylonian Collection); Plimpton (George A. Plimpton Collection, Universidade Columbia); VAT (Vorderasiatische Abteilung, Tontafeln, Staatliche Museen, Berlim).”
“Os registros disponíveis são mais numerosos para a matemática mesopotâmica do que para a egípcia, provavelmente devido à maior facilidade na preservação da argila usada pelos mesopotâmicos do que do papiro, usado pelos egípcios.”
“A escrita, no período faraônico, tinha dois formatos: hieroglífico e hierático. O primeiro era mais utilizado nas inscrições monumentais em pedra; o segundo era uma forma cursiva de escrita, empregada nos papiros e vasos relacionados a funções do dia a dia, como documentos administrativos, cartas e literatura. Os textos matemáticos eram escritos em hierático e datam da primeira metade do segundo milênio [antes de Cristo], apesar de haver registros numéricos anteriores.”
“Høyrup (…) mostrou que a <álgebra> dos babilônicos estava intimamente relacionada a um procedimento geométrico de <cortar e colar>. Logo, tal prática não poderia ser descrita como álgebra, sendo mais adequado falar de <cálculos com grandezas>.”
“Centenas de tabletes arcaicos indicavam que a escrita já existia no quarto milênio, pois continham sinais traçados ou impressos com um determinado tipo de estilete. O material contradizia a tese pictográfica, pois nessa fase inicial da escrita as figuras que representavam algum objeto concreto eram exceção. Diversos tabletes traziam sinais comuns que eram abstratos, isto é, não procuravam representar um objeto. Assim, o sinal para designar uma ovelha não era o desenho de uma ovelha, mas um círculo com uma cruz.”
“Eles não representavam números, como 1 ou 10, mas eram instrumentos particulares que serviam para contar cada tipo de insumo: jarras de óleo eram contadas com ovóides; pequenas quantidades de grãos, com esferas. Os tokens eram usados em correspondência um a um com o que contavam: uma jarra de óleo era representada por um ovóide; duas jarras, por dois ovóides; e assim por diante.” “Isso quer dizer que o fato de associarmos um mesmo símbolo, no caso 1, ou um cone, a objetos de tipos distintos, como ovelhas e jarras de óleo, consiste em uma abstração que não estava presente no processo de contagem descrito anteriormente.”
“A descoberta dos tabletes de Uruk levou ao desenvolvimento de um projeto dedicado à sua interpretação, que começou por volta dos anos 1960, em Berlim. A iniciativa foi fundamental para a compreensão dos símbolos encontrados e deu origem à obra que esclareceu o contexto desses registros: Archaic Bookkeeping: Early Writing and Techniques of Economic Administration in the Ancient Near East (Contabilidade arcaica: escrita antiga e técnicas de administração econômica no antigo Oriente Próximo), de H.J. Nissen, P. Damerow e R.K. Englund. Ficou claro, a partir daí, que os registros serviam para documentar atividades administrativas e exibiam um sistema complexo para controlar as riquezas, apresentando balanços de produtos e contas.”
“Havia mais de 6 sistemas de capacidade usados para diferentes tipos de grãos e de líquidos. Ao passo que os objetos discretos eram contados em base 60, a contagem de outros produtos empregava a base 120. Além disso, havia métodos distintos para contar tempo e áreas.”
“Uma cunha pequena representava uma unidade de grãos, a unidade básica do sistema de medidas dos sumérios. Uma quantidade 6x maior era representada pela marca circular, e outra 10x maior que esta última, por um círculo maior”
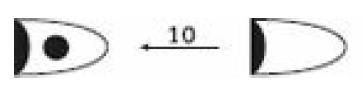

ESTILO PROTOCUNEIFORME
(Ler da direita para a esquerda. – As imagens não são ‘números’ como no Ocidente, apenas de forma algo relativa. – Na 1ª imagem-seqüência [figura], demonstra-se uma figura que é um dez avos de outra e portanto outra que é 10x a primeira; na segunda figura assume-se a representação numérica abstrata ocidental para facilitar o raciocínio, entre aspas – a unidade “10”, que podia ser qualquer outro número inteiro ou fração, seis vezes menor que a unidade “60”, esta 10x menor que a unidade “600”, e assim por diante. Como a primeira imagem da 2ª figura difere da primeira imagem da 1ª figura, bem como da 2ª imagem da 1ª figura – mas note-se a semelhança da bola preta que na figura mais acima é apenas uma parte de um todo maior, indicando uma lógica interna –, vê-se que a representação numérica ou contagem pode iniciar de qualquer representação simbólica.)
TRANSIÇÃO AO ESTILO CUNEIFORME “MADURO”
Aparição das primeiras notações fixas

= 1
(cunha simples)

= 10
(ponto ou esfera)

= 60
(cunha aumentada)

= 600
(cunha com ponto ou esfera)

= 3600
(ponto aumentado ou esfera aumentada)

= 36000
(ponto dentro de outro ponto / esfera dentro de outra esfera / notação dos 3 círculos preto e branco contrastados em relação de contido e contém / ou ainda “esfera com raias”)
Outras notações foram aparecendo:

Fase tardia da evolução (reprise intercalada dos sinais, a cada multiplicação por 60):

Toda simplificação é uma complexificação!
“O sistema sexagesimal posicional usado no período babilônico deve ter surgido da padronização desse sistema numérico, antes do final do terceiro milênio [a.C.]. Ainda que a representação numérica continuasse a ser dependente do contexto e a usar diferentes bases ao mesmo tempo, aos poucos começaram a ser registradas listas que resumiam as relações entre diferentes sistemas de medida.”

“Na verdade, presume-se que muitos dos tabletes que nos fornecem um conhecimento sobre a matemática babilônica tinham funções pedagógicas.”
“Sobre a tradução dos textos cuneiformes, ver Gonçalves, Observações sobre a tradução de textos matemáticos cuneiformes.”
“O sistema que usamos para representar as horas, os minutos e os segundos é um sistema sexagesimal [o nosso possui literalmente 60 valores, já que 0 = 60; o cuneiforme, 59, já que não há o zero e 1 = 60.].”
“Nosso sistema de numeração de base 10 também é posicional. Há símbolos diferentes para os números de 1 a 9, e o 10 é representado pelo próprio 1, mas em uma posição diferente. Por isso se diz que nosso sistema é um sistema posicional de numeração de base 10, o que significa que a posição ocupada por cada algarismo em um número altera seu valor de uma potência de 10 para cada casa à esquerda.”
“Se considerarmos 125 escrito na base 60, estaremos representando 1 × 60² + 2 × 60¹ + 5 × 600, que é igual a 3725 na base 10.”
“Suponhamos agora que, em vez de usar a base 10, queiramos escrever um número em um sistema de numeração posicional cuja base genérica é b. Para representar um número N qualquer nessa base b, escrevemos:
N = anbn + an−1bn−1 + … + a0b0 + a−1b−1 + … + a−mb−m + ….
Isso significa que anbn + an−1bn−1 + … + a0b0 é a parte inteira e temos que a−1b−1 + … + a−mb−m + … é a parte fracionária desse número.”
“Como na base 60 podemos ter, em cada casa, algarismos de 1 a 59, empregaremos o símbolo ; como separador de algarismos dentro da parte inteira ou dentro da parte fracionária de um número.” “Por exemplo, no número 12;11,6;31 a parte inteira é constituída por dois algarismos (12 e 11); e a parte fracionária por outros dois (6 e 31).”
12;11 neste caso = no nosso sistema a:
12 x 60¹ + 11 x 600 =
12 x 60 + 11 =
720 + 11 =
731
O número após a vírgula 6;31 assim se resolve:
6 x 60-1 + 31 x 60-2 =
6 x 1/60 + 31 x 1/3600 =
6/60 + 31/3600 =
1/10 + 0,00861… =
0,10861…
Logo, 12;11,6;31 =
731 + ~0,10861 =
~731,1086 =
~731,11
“Que mecanismo utilizamos em nosso sistema de numeração para indicar a posição de um símbolo? Por exemplo, como fazemos para que o 1 do número 1 tenha um valor distinto do 1 do número 10?”

“Observe-se que esse sistema dá margem a algumas ambigüidades. Por exemplo, o mesmo símbolo podendo ser lido como (1 + 1) ou (1;1) [ou seja, como 2 ou 61 da notação decimal]. (…) Nesse caso, houve uma época em que se usava o símbolo com tamanhos diferentes para representar o 60 e o 1, hábito que talvez esteja na origem do sistema posicional.” Quer seja: sem escala ou casas decimais, ficamos incapacitados de resolver informações polissêmicas, a não ser que, por exemplo, fosse evidente, digamos, pelo número de cabeças visíveis num rebanho, a qual grandeza o símbolo faria referência.
“Algumas vezes era deixado um espaço entre os dois símbolos para marcar uma coluna vazia. Mas essa solução não resolve o problema de expressar uma coluna vazia no fim do número, logo, permite diferenciar 7200 de 3601, p.ex., mas não 7200 de 2 e de 120.”
ADIÇÃO EM BASE 60
1;30,27;40 + 29,15;13 = 1;59,42;53
1;59 + 1 = 2
MULTIPLICAÇÃO EM BASE 60
4 x 20 = 1;20
DIVISÃO EM BASE 60
1,30 ÷ 3 =0,30
(raciocínio análogo a: 1h30 dividido por 3 é igual a meia-hora. A coisa se complicaria muito se o segundo número possuísse casa fracionária [sessentesimal e não decimal].)
Por óbvio, multiplicações, divisões, somas e subtrações por 60 são as operações mais simples.
“Uma das vantagens do sistema sexagesimal é o fato de que o número 60 é divisível por todos os inteiros entre 1 e 6, o que facilita a inversão dos números expressos nessa base. A divisibilidade por inteiros pequenos é uma importante característica a ser levada em conta no momento da escolha de uma base para representar os números. A base 12 está presente até hoje no comércio, onde usamos a dúzia justamente pelo fato de o número 12 ser divisível por 2, 3 e 4 ao mesmo tempo. Não podemos dizer, no entanto, que esse tenha sido o motivo do emprego dessa base pelos mesopotâmicos.”
“No sistema posicional, podem-se usar os mesmos símbolos para escrever números inteiros e números fracionários, o que não acontece no sistema egípcio, como veremos adiante.”
“Uma grande vantagem do sistema posicional é permitir a escrita de números muito grandes com poucos símbolos. Efetivamente, mais tarde, quando os babilônios iniciaram seus estudos astronômicos, tornou-se necessário escrever números maiores, fazendo com que as características posicionais se tornassem mais evidentes.”
“A observação dos corpos celestes, presente nos registros da matemática babilônica do primeiro milênio a.C., bem como a aritmética e o sistema posicional sexagesimal usados nesse contexto, pode ter tido influência sobre a tradição grega de Hiparco e Ptolomeu. A astronomia desenvolvida por eles no Egito, na virada do milênio, indica que os cálculos astronômicos e trigonométricos de então eram feitos por meio do sistema sexagesimal posicional, ainda que com uma simbologia distinta, e que este permaneceu sendo o principal sistema até a introdução do sistema decimal indo-arábico, muitos séculos depois. Apesar disso, a idéia de que teria havido uma continuidade entre as matemáticas mesopotâmica e grega foi construída com base em interpretações equivocadas e não há evidências nítidas da influência dos mesopotâmicos sobre a tradição grega.”
“Os astrônomos selêucidas, talvez pela necessidade de lidar com números grandes, chegaram a introduzir um símbolo para designar o zero, ou melhor, uma coluna vazia. No caso de 3601, escrevia-se 1; separador; 1. O separador era simbolizado por dois traços inclinados:
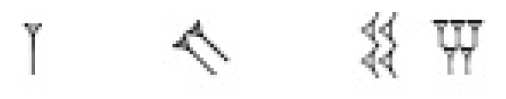
1 ; // ; 1 =
3601
“A noção de zero como número só surgirá quando ele começar a ser associado a operações, em particular, ao resultado de uma operação, como 1 – 1 = 0. Escrever uma história do zero é tarefa bastante complexa, pois devem ser levados em conta, antes de tudo, os diversos contextos em que ele aparece e o que essa noção pode significar em cada contexto.”
“No caso da multiplicação, o uso de tabuadas em tabletes era fundamental. Basta observar que os cálculos elementares, ou seja, aqueles que correspondem à nossa tabuada, incluem multiplicações até 59 × 59! Isso pode indicar a necessidade de tabletes mesmo para os cálculos mais elementares.
Um exemplo de tablete de multiplicação por 25:
1 (vezes 25 é igual a) 25
2 (vezes 25 é igual a) 50
3 (vezes 25 é igual a) 1;15
4 (vezes 25 é igual a) 1;40
5 (vezes 25 é igual a) 2;05
6 (vezes 25 é igual a) 2;30
7 (vezes 25 é igual a) 2;55 etc.”
“O procedimento de divisão empregado pelos babilônios nos leva a concluir que a utilização dos tabletes, nesse caso, não servia apenas à memorização de tabuadas, o que seria um papel acessório. Para que a técnica adotada na divisão fosse rigorosa, devia haver uma necessidade intrínseca de se representar em tabletes as divisões por números cujos inversos não possuem representação finita em base 60. Isso porque, no caso de 1/N não possuir representação finita, o resultado da divisão de M por N teria de estar registrado em um tablete. Se essa operação fosse realizada pelo procedimento usual, ou seja, multiplicando-se M por 1/N, o resultado obtido não seria correto, da mesma forma que não seria correto fazer 6 × 0,3333…(=1/3) para dividir 6 por 3.”
“Além das operações de soma, subtração, multiplicação e divisão, os babilônios também resolviam potências e raízes quadradas e registravam os resultados em tabletes. O método usado nesse último caso era bastante interessante, uma vez que permitia obter valores aproximados para raízes que hoje sabemos serem irracionais.”
“Além dos tabletes contendo o resultado de operações, os babilônios tinham um certo número de tabletes de procedimentos, como se fossem exercícios resolvidos. Correspondiam a problemas que trataríamos hoje por meio de equações. Analisaremos alguns deles em detalhes, com a finalidade de mostrar como seria anacrônico considerar que os babilônios soubessem resolver equações.”
“A generalidade dos algoritmos babilônicos é distinta, pois eles constroem uma lista de exemplos típicos, interpolando-os, em seguida, para resolver novos problemas.”
“Desde a época grega, e pelo menos até o século XVII, a geometria teve de respeitar a homogeneidade das grandezas. Isso quer dizer que não era permitido somar uma área com um segmento de reta. A operação utilizada pelos babilônios revela que eles não experimentavam nenhuma dificuldade nesse sentido, uma vez que possuíam um modo concreto de transformar um segmento de reta em um retângulo, operação traduzida aqui como <projeção>.”
“Exemplos como esse, envolvendo operações de <cortar e colar> figuras geométricas parecem ter sido comuns na época. Høyrup caracteriza essas práticas como uma <geometria ingênua>.”
“Se definíssemos álgebra como um conjunto de procedimentos que devem ser aplicados a entidades matemáticas abstratas, poderíamos até concluir que os babilônios realizavam uma álgebra de comprimentos, larguras e áreas. Mas, nesse caso, deveríamos ter o cuidado de definir a álgebra dos babilônios de um modo particular, e não por extensão do nosso conceito moderno de álgebra.”
“O sistema decimal egípcio já estava desenvolvido por volta do ano 3000 [a.C.], ou seja, antes da unificação do Egito sob o regime dos faraós. O número 1 era representado por uma barra vertical, e os números consecutivos de 2 a 9 eram obtidos pela soma de um número correspondente de barras. (…) O número 10 é uma alça [parece um pórtico ou uma ferradura apontando para o céu]; 100, uma espiral; mil, a flor de lótus; 10 mil, um dedo; 100 mil, um sapo; e 1 milhão, um deus com as mãos levantadas.” Quanta inocência! Ou serei eu muito malicioso? Veja abaixo…
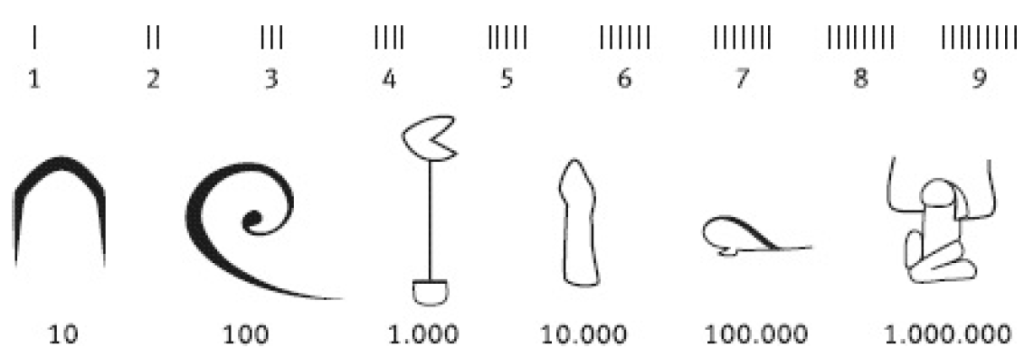
Impossível não associar a notação egípcia a motivos religiosos ou sexuais – particularmente o 10 mil (caractere fálico) e o 1 milhão (duas interpretações instantâneas: 1- mão segura pênis e realiza-se, no topo, felação; 2- analogamente, pessoa ajoelhada em prece, com braços soerguidos), mas também o 100 mil, que remete a girino, embora não possamos dizer que se soubesse o formato de um espermatozóide (nem por isso deixava de haver uma noção, comprovada mitologicamente, de que ‘a vida veio da água’).
“os números são obtidos pela soma de todos os números representados pelos símbolos (sistema aditivo) (…) esse sistema não é adequado para representar números muito grandes (…) Cabe notar que os romanos lidavam com números grandes [mesmo] usando um sistema aditivo, o que relativiza esta afirmação.”
Somente as frações ½, 1/3, 2/3 e ¼ possuíam símbolos próprios (exclusivos).
“Nosso numerador indica quantas partes estamos tomando de uma subdivisão em um dado número de partes. Na designação egípcia, o símbolo oval [uma espécie de auréola sobre o símbolo usual do número] não possui um sentido cardinal, mas ordinal. Ou seja, indica que, em uma distribuição em n partes iguais, tomamos a n–ésima parte, aquela que conclui a subdivisão em n partes. É como se estivéssemos distribuindo algo por n pessoas e 1/n é quanto cada uma irá ganhar. Logo, configura-se um certo abuso de linguagem dizer que, na representação egípcia, as frações possuem ‘numerador 1’. Seria mais adequado dizer que essas frações egípcias representam os inversos dos números.”
Como eles representavam frações de numerador >1?
R: 5/8 seriam ½ + 1/8. (I)
Outros ex.:
(II) 58/87 = ½ + 1/6
(III) 3/7 = 1/3 + 1/11 + 1/231
“Se quisermos saber, em nossa representação, qual a maior de duas frações teremos de igualar os denominadores. Na representação egípcia, uma inspeção direta permite dizer qual a maior das duas frações”
“A palavra <aha> é traduzida por <número> ou <quantidade>, e esses problemas eram procedimentos para encontrar uma quantidade desconhecida quando é dada uma relação com um resultado conhecido.”
O INÍCIO DAS SUPERSTIÇÕES SOBRE “NÚMEROS RUINS”? “a duplicação de frações de denominador ímpar, um cálculo ‘difícil’, era realizada apenas uma vez, e sempre que se necessitasse do resultado recorria-se às tabelas. Pelo mesmo motivo, as somas de frações também traziam dificuldade e deviam ser representadas em tabelas.”
“Esses exemplos são citados em diversos livros, muitas vezes com o objetivo de indicar que os povos babilônicos e egípcios possuíam aproximações para o valor de π. Nosso objetivo é entender em que contexto tais problemas se inserem e em que medida podem ser ou não considerados instâncias primitivas da utilização de π. Para abreviar, evitamos entrar em detalhes sobre as unidades de medida utilizadas.”
“Exemplo egípcio (Problema 41 do papiro de Rhind): <Fazer um celeiro redondo de 9 por 10.> O celeiro tem o formato de um cilindro e a primeira parte do problema consiste em calcular a área da base, em forma de circunferência, cujo diâmetro é 9. A segunda parte consiste em calcular o volume em grãos se a altura é 10. O procedimento para resolver a primeira parte é o seguinte:
1) Subtraia 1/9 de 9. Resta: 8.
2) 8*8 = 64
A1 = 64
“O valor 1/9 é uma constante que devia ser aprendida e utilizada sempre que se quisesse calcular a área de uma circunferência (multiplicando essa constante pelo diâmetro). (….) O resultado deveria ser multiplicado por ele mesmo”
No ocidente:
A = π*R² = (8/9*d)² = (8/9*2)²*r²,
em que d é o diâmetro dado.
π = ~3,16,
“Daí a afirmação, apressada, contida em alguns livros de história, de que os egípcios já possuíam uma aproximação para π.”
“Exemplo babilônico (Haddad 104): <Procedimento para um tronco. Sua linha divisória é 0,05. Quanto ele pode armazenar?>”
“<Linha divisória> é o diâmetro da circunferência determinada por uma seção transversal. Em primeiro lugar, calculava-se a área de uma seção transversal, de forma circular:
1) Triplique a linha divisória:
3*0,05 = 0,15
2) Faça o quadrado de 0,15:
(0,15)² = 0,03;45
3) Multiplique 0,03;45 novamente pela linha divisória:
Abase = 0,03;45*0,05 = 0,00;18;45
4) Multiplicar a área da base pela altura:
Abase*Alt.
“A altura era considerada implicitamente como igual ao diâmetro.”
“Lembramos que a fórmula usada atualmente para o perímetro da circunferência é 2πr = πd (onde d é o diâmetro). Poderíamos dizer que o método dos babilônios não está muito longe do nosso, usando 3 como valor aproximado de π. Mas o objetivo não é calcular o perímetro e sim a área da circunferência, que, em seguida, deverá ser multiplicada pela altura. Para calcular a área a partir do perímetro, temos de elevar ao quadrado e depois dividir o resultado por 4π (basta verificar na nossa fórmula que a área πr² = (π²*d²)/4π). Mas, considerando que os babilônios usavam 3 como constante, em base 60, dividir por 4π é equivalente a multiplicar por 0,5 (pois 1/4π = 1/12 = 5/60 é o mesmo que 0,5 em base 60). Isso explica a multiplicação por essa constante”
“Seria um tremendo anacronismo dizer que os povos mesopotâmicos e egípcios já possuíam uma estimativa para π, pois esses valores estavam implícitos em operações que funcionavam, ao invés de serem expressos por números considerados constantes universais, como em nossa concepção atual sobre π.”
“Contar, e registrar quantidades, pode ser dita uma atividade concreta, pois implica um corpo a corpo com os objetos contados. Quando os tokens eram manipulados na contagem, e mesmo quando eram impressos na superfície dos invólucros, essa concretude estava em jogo. A abstração tem lugar a partir do momento em que o conteúdo dos invólucros podia ser esquecido, levando a um registro independente do que estava sendo contado, impresso em tabletes.”
“É MUITO COMUM LERMOS que a geometria surgiu às margens do Nilo, devido à necessidade de medir a área das terras a serem redistribuídas, após as enchentes, entre os que haviam sofrido prejuízos. Essa hipótese tem sua origem nos escritos de Heródoto, datados do século V a.C.: <Quando das inundações do Nilo, o rei Sesóstris enviava pessoas para inspecionar o terreno e medir a diminuição dos mesmos para atribuir ao homem uma redução proporcional de impostos. Aí está, creio eu, a origem da geometria, que migrou, mais tarde, para a Grécia>” “Além disso, quase todos os livros de história da matemática a que temos acesso em português reproduzem a lenda de que a descoberta dos irracionais provocou uma crise nos fundamentos da matemática grega. Alguns chegam a afirmar que tal crise só foi resolvida com a definição rigorosa dos números reais, proposta por Cantor e Dedekind no século XIX (ou seja, mais de vinte séculos depois).”
Matemáticos célebres da Grécia Antiga em ordem cronológica:
1. Tales
2. Pitágoras
3. Euclides
CAPÍTULO 2. Lendas sobre o início da matemática na Grécia
“O testemunho de Heródoto, apresentado no segundo dos nove livros de suas Histórias, se insere em uma descrição dos costumes e das instituições de povos diversos e é parte das investigações sobre as causas das guerras entre gregos e bárbaros (pertencentes ao império persa). Esse segundo livro é inteiramente consagrado ao Egito e nele se encontra a menção à palavra grega <geometria>. Os egípcios teriam revelado que seu rei partilhava a terra igualmente entre todos, contanto que lhe fosse atribuído um imposto na base dessa repartição. Como o Nilo, às vezes, cobria parte de um lote, era preciso medir que pedaço de terra o proprietário tinha perdido, com o fim de recalcular o pagamento devido.” “A palavra geometria pode ser traduzida, portanto, como <medida da terra>. Vem daí a idéia de que seu surgimento está ligado à agrimensura.”
“Mas que gregos teriam levado a geometria para a Grécia? Heródoto não diz nada sobre o assunto e estudiosos postularam, posteriormente, que teria sido Tales. Para tornar o relato mais consistente, afirmou-se que esse matemático teria calculado até mesmo a altura de uma das pirâmides do Egito. Tal anedota, que Eudemo e Proclus ajudaram a construir, combina a idéia de que a geometria prática, de origem egípcia, teria evoluído para a determinação indireta de medidas inacessíveis, caso da altura de uma pirâmide.”
“Não há uma documentação confiável que possa estabelecer a transição da matemática mesopotâmica e egípcia para a grega. Essa é, na verdade, uma etapa na construção do mito de que existiria uma matemática geral da humanidade.”
“A designação de ‘abstrato’ ganha, agora, um sentido diferente do exposto no Capítulo 1, já que aqui a expressão está associada à prática geométrica e não numérica. O registro grego é fragmentário e a escassez de fontes faz com que o trabalho do historiador pareça especulativo. Existem alguns tratados matemáticos concluídos, outros parcialmente finalizados e outros, ainda, com apenas trechos aleatórios preservados acidentalmente em obras derivadas, além de alguma literatura sobre a matemática em textos filosóficos.”
“Alguns termos de geometria já apareciam, por exemplo, na arquitetura. Há escritos técnicos do século VI abordando problemas relacionados à astronomia e ao calendário.”
“é difícil estabelecer as bases factuais desta e de outras afirmações sobre Tales atribuídas por Proclus a Eudemo. Na verdade, o papel de Tales foi objeto de algumas controvérsias históricas. Segundo W. Burkert, parece ser fato que, por volta do século V, seu nome era empregado em conexão com resultados geométricos. Além disso, Aristóteles menciona Tales na Metafísica como o fundador da filosofia.”
“A historiografia da matemática costuma analisar, entre as épocas de Tales e de Euclides, as contribuições da escola pitagórica do século V. Os ensinamentos dessa escola teriam influenciado um outro matemático importante desse século, Hipócrates de Quios. Além disso, é frequente encontrarmos referências a Pitágoras como um dos primeiros matemáticos gregos. Mas ambas as afirmações são hoje largamente questionadas pelos historiadores.”
“Se o matemático mais conhecido do século V, Hipócrates de Quios, não era herdeiro de Pitágoras, de onde veio sua matemática? As evidências mostram que havia uma matemática grega antes dos pitagóricos. Em meados desse século, tal prática parecia estar no centro dos interesses dos principais pensadores, pois muitos deles se conectavam com questões matemáticas, caso de Anaxágoras, Hípias e Antifonte. (…) Em Atenas, a geometria era ensinada, apesar de não sabermos exatamente como. Nos diálogos de Platão, há algumas evidências da existência de um ambiente de discussão sobre os problemas geométricos que data de uma época anterior a sua obra. Um exemplo são os diálogos entre Sócrates e Teodoro, que era contemporâneo de Hipócrates e de quem Teeteto, importante personagem dos textos de Platão, deve ter sido aluno.”
“como mostra W. Burkert, a escola pitagórica não parece ter tido um papel significativo na transformação da matemática de seu tempo. A convicção de que o pitagorismo está na fonte da matemática grega decorre da tradição educacional dos neopitagóricos e neoplatônicos da Antiguidade, durante os primeiros séculos da era cristã.” Curioso.
“Neste capítulo e no próximo mostraremos que a visão de que a matemática abstrata, que faz uso de demonstrações, foi uma invenção dos gregos toma por base os Elementos de Euclides. Logo, seria anacrônico analisar o desenvolvimento da matemática antes de Euclides a partir de inferências lógicas.”
“Mesmo o famoso teorema ‘de Pitágoras’, em sua compreensão geométrica como relação entre medidas dos lados de um triângulo retângulo, não parece ter sido particularmente estudado por Pitágoras e sua escola. Veremos, ainda, que a descoberta das grandezas incomensuráveis, freqüentemente atribuída a um pitagórico, deve ter tido outras origens. Tal descoberta contribuiu para a separação entre a geometria e a aritmética, a primeira devendo se dedicar às grandezas geométricas e a segunda, aos números – separação que é um dos traços marcantes da geometria grega, ao menos na maneira como ela se disseminou com Euclides.”
“Um de nossos principais objetivos, aqui, é desconstruir os mitos envolvidos na chamada ‘crise dos incomensuráveis’. Essa tese tem origem em obras já ultrapassadas que constituem um exemplo paradigmático de um modo de fazer história da matemática – hoje contestado – baseado em pressupostos modernos sobre a natureza dessa disciplina. As narrativas sobre o suposto escândalo provocado pela descoberta dos incomensuráveis citam também os paradoxos de Zenão, por isso descreveremos brevemente seus enunciados, mostrando que estes tinham um fim filosófico e não matemático.”
“A Antiuidade tardia nos legou 2 textos de pensadores neoplatônicos nos quais os feitos da matemática grega foram avaliados: um de Jâmblico, De communi mathematica scientia (Sobre o conhecimento matemático comum), e outro de Proclus, o primeiro prólogo ao seu Comentário sobre o primeiro livro dos Elementos de Euclides. Jâmblico viveu entre os séculos III e IV d.C. (…) De communi mathematica scientia é o terceiro volume de uma obra maior, dedicada ao pitagorismo, De vita pytaghorica (Sobre a vida pitagórica)” “A escassez das fontes, somada à convergência interessada dos únicos textos disponíveis, nos permite duvidar até mesmo da existência de um matemático de nome Pitágoras.”
“A matemática atribuída a Pitágoras é a aritmética de pontinhos, que será detalhada adiante, mas não se sabe ao certo se ela é uma criação de um matemático chamado Pitágoras, de integrantes de uma escola antiga chamada pitagórica (mas não de Pitágoras), ou dos neoplatônicos e neopitagóricos da Antiguidade, como Jâmblico e Nicômaco.”
“Os pitagóricos embora sejam vistos como os primeiros a considerar o número do ponto de vista teórico, e não apenas prático, não possuíam, de fato, uma noção de número puro. Diferentemente de Platão, os pitagóricos não admitiam nenhuma separação entre número e corporeidade, entre seres corpóreos e incorpóreos.”
“O Um é ao mesmo tempo par e ímpar, ser bissexuado a partir do qual os outros números se desenvolveram. O par e o ímpar são elementos dos números e na conjugação limitado-ilimitado está a oposição cósmica primordial por trás do mundo, expresso em números.”
“As relações entre os números não representavam, portanto, uma cadeia linear na qual todas as relações internas eram semelhantes. Cada arranjo designava uma ordem distinta, com ligações próprias. Daí o papel dos números figurados na matemática pitagórica. Esses números eram, de fato, figuras formadas por pontos, como as que encontramos em um dado. Não é uma cifra, como 3, que serve de representação pictórica para um número, mas a delimitação de uma área constituída de pontos, como uma constelação.”

“Os números triangulares representados na Figura 1 podem ser associados aos nossos números 1, 3, 6, 10, 15 e 21, que possuem, respectivamente, ordem n = 1, 2, 3, 4, 5 e 6. Em linguagem atual, o número triangular de ordem n é dado pela soma da progressão aritmética 1 + 2 + 3 + … + n = [n*(n+1)]/2. Em seguida, temos os números quadrados, que, em nosso simbolismo, podem ser escritos como n².”

Essa imagem, chamada gnomons, é a representação pitagórica equivalente à nossas equações:
1² + 3 = 2²
2² + 5 = 3²
3² + 7 = 4² (4º gnomon, etc.)
“Temos notícia de que a ciência matemática era dividida, primeiramente, em duas partes: uma que tratava dos números; outra, das grandezas. Cada uma era subdividida em duas outras partes: a aritmética estudava as quantidades em si mesmas; a música, as relações entre quantidades; a geometria, as grandezas em repouso; e a astronomia, as grandezas em movimento inerente. O conhecimento sobre esse aspecto da doutrina pitagórica vem da Metafísica de Aristóteles”
“Ar. usava essa tabela de opostos para criticar a separação binária platônica segundo a qual, de um lado, temos o igual, imóvel e harmônico e, de outro, o desigual, movente e desarmônico.” Que pena que não se encontre isso em lugar nenhum do cânone platônico!
“Para Aristóteles, isso indicaria a presença de seres abstratos. Por exemplo, a partir do tetractys [o terceiro triângulo de duas imagens acima, aquele com 10 pontos] os pitagóricos teriam obtido as entidades abstratas: ponto, reta, plano e sólido. No entanto, Burkert nota que essa tese está em franca contradição com outra afirmação do próprio Aristóteles, a saber, que não havia entre os pitagóricos a noção de ponto, no sentido geométrico do termo.”
“O enunciado mais famoso associado ao nome de Pitágoras é o teorema que estabelece uma relação entre as medidas dos lados de um triângulo retângulo: <O quadrado da hipotenusa é igual à soma dos quadrados dos catetos>. Hoje se sabe que essa relação era conhecida por diversos povos mais antigos do que os gregos e pode ter sido um saber comum na época de Pitágoras. No entanto, não é nosso objetivo mostrar que os pitagóricos não foram os primeiros na história a estabelecer tal relação. O objetivo é investigar de que modo esse resultado podia intervir na matemática praticada pelos pitagóricos, com as características anteriormente descritas. A demonstração desse teorema, encontrada nos Elementos de Euclides, faz uso de resultados que eram desconhecidos na época da escola pitagórica. Não se conhece nenhuma prova do teorema geométrico que tenha sido fornecida por um pitagórico e parece pouco provável que ela exista.”
“Não deve ter havido um teorema geométrico sobre o triângulo retângulo demonstrado pelos pitagóricos, e sim um estudo das chamadas triplas pitagóricas. O problema das triplas pitagóricas é fornecer triplas constando de dois números quadrados e um terceiro número quadrado que seja a soma dos dois primeiros.¹ Essas triplas são constituídas por números inteiros que podem ser associados às medidas dos lados de um triângulo retângulo.
¹ Alguns historiadores da matemática defendem que na placa Plimpton 322 há um indício de que os babilônios já estudavam as triplas pitagóricas, o que mostraria que a relação atribuída a Pitágoras seria conhecida na Babilônia pelo menos mil anos antes dele. Essa tese é questionada por E. Robson em ‘Neither Sherlock Holmes nor Babylon: A reassessment of Plimpton 322’ e ‘Words and pictures: new light on Plimpton 322’.”
“Provavelmente, os pitagóricos chegaram a essas triplas por meio do gnomon”
“a primeira tripla pitagórica: (3, 4, 5).” = 3² + 4² = 5²
“Na tradição, poucas triplas são mencionadas e (3, 4, 5) tem um papel especial, pois 3 é o macho; 4, a fêmea; e 5, o casamento que os une no triângulo pitagórico. Segundo Proclus, havia 2 métodos para se obter triplas pitagóricas: um de Pitágoras, outro de Platão. O primeiro começa pelos números ímpares. Associando um dado número ao menor dos lados do triângulo que formam o ângulo reto, tomamos o seu quadrado, subtraímos a unidade e dividimos por 2, obtendo o outro lado, que forma o ângulo reto. Para obter o lado oposto, somamos a unidade novamente ao resultado. Seja 3, por exemplo, o menor dos lados. Toma-se o seu quadrado e subtrai-se a unidade, obtendo 8, e extrai-se a metade de 8, que é 4. Adicionando a unidade novamente, obtemos 5, e o triângulo retângulo que procuramos é o de lados 3, 4 e 5.
O método platônico começa por um número par, considerado um dos lados que formam o ângulo reto. Primeiro dividimos esse número por 2 e fazemos o quadrado de sua metade. Subtraindo 1 desse quadrado, obtemos o outro lado que forma o ângulo reto e, adicionando 1, o lado restante. Por exemplo, seja 4 o lado. Dividimos por 2 e tomamos o quadrado da metade, obtendo 4. Subtraímos 1 e adicionamos 1, obtendo os lados restantes: 3 e 5.” Em linguagem moderna, o método platônico = (2a)² + (a² − 1)² = (a² + 1)².
“Logo, pelo contexto em que esse resultado intervém, não é possível dizer que o conhecimento aritmético das triplas pitagóricas seja o exato correlato do teorema geométrico atribuído a Pitágoras, daí as aspas empregadas aqui ao falarmos do teorema <de Pitágoras>.”
“A versão mais popular é a de que esse livro de Euclides resulta de uma compilação de conhecimentos matemáticos anteriores, ainda que a forma da exposição deva ser característica do tempo e do meio em que ele viveu. Não é possível confirmar essa tese, mas é fato que uma boa parte da matemática contida nessa obra associa-se a outros trabalhos gregos. Euclides apresenta 2 tipos de teoria das razões e proporções. Há uma versão no livro VII que pode ser aplicada somente à razão entre inteiros e é atribuída aos pitagóricos. A definição contida aí é usada para razões entre grandezas comensuráveis. A segunda versão, presumidamente posterior à primeira, está no livro V e é atribuída ao matemático platônico Eudoxo. Essa última teoria das razões e proporções é bastante sofisticada e se aplica igualmente a grandezas comensuráveis e incomensuráveis.”
“Segundo Knorr, o desenvolvimento formal da matemática deve ter se iniciado com os trabalhos de Teeteto, no início do século IV”
“Hipócrates teria sido o autor da primeira obra escrita em um livro de ‘elementos’, ou seja, com a apresentação sistemática da geometria. Infelizmente, poucos fragmentos sobreviveram. Seu trabalho mais conhecido é o estudo das lúnulas, que são porções de círculo compreendidas entre duas circunferências, incluindo a investigação de quadraturas. Os escritos de Hipócrates constituem o único documento do século V contendo um estudo de razões e proporções entre figuras geométricas. Ele sabia que a razão entre as áreas de dois segmentos de círculo semelhantes é igual à razão entre os quadrados de seus diâmetros. Essa demonstração, de uma época bem anterior à de Eudoxo, exigia um conhecimento profundo de razões e proporções.”
“A palavra antifairese vem do grego e significa, literalmente, subtração recíproca. Na álgebra moderna, o procedimento é semelhante ao conhecido como <algoritmo de Euclides> e sua função é encontrar o maior divisor comum entre dois números.”
“O método da antifairese descreve uma série de comparações. Por exemplo, podemos pedir a um aluno que compare duas pilhas de pedras. Se a primeira tem 60 e a segunda, 26, concluímos que:
1) da primeira pilha com 60 pedras é possível subtrair duas vezes a pilha com 26 pedras, e ainda resta uma pilha com 8 pedras;
2) da pilha com 26 pedras é possível subtrair três vezes a pilha com 8 pedras, e ainda resta uma pilha com 2 pedras;
3) por fim, a pilha com 2 pedras cabe, exatamente, quatro vezes na pilha com 8 pedras.
A sequência <2x, 3x e 4x exatamente> representa o número de subtrações que se pode fazer em cada passo. Podemos chamá-la de razão e usar a notação Ant (60, 26) = [2, 3, 4] para representar a razão antifairética 60:26. A escolha de grandezas que permitem uma representação finita por números inteiros nem sempre é possível.
Para Fowler, os gregos entendiam a razão 22:6, por exemplo, baseados no fato de que é possível subtrair 6 de 22 três vezes, restando 4; em seguida, subtrai-se 4 de 6, restando 2; finalmente, subtrai-se 2 de 4 exatamente duas vezes. Logo, a razão 22:6 seria definida pela sequência <3x, 1x, 2x>.”
“Essa antifairese equivale a fazer A = n0B + R1, em seguida, B = n1R1 + R2, depois R2 = n1R2 + R3, e assim por diante. O procedimento pode ou não chegar ao fim. Quando ele termina, a medida comum aos dois segmentos fica associada a um terceiro segmento, R, que é o último resto não-nulo encontrado e que mede os segmentos A e B. Isso permite achar a medida comum a 2 segmentos e, assim, é possível reduzir a geometria à aritmética, pois cada segmento será representado por sua medida.”
“A teoria das grandezas comensuráveis foi desenvolvida, primeiramente, pela aritmética e, depois, por imitação, pela geometria. Por essa razão, ambas as ciências definem grandezas comensuráveis como aquelas que estão uma para outra na razão de um número para outro número, o que implica que a comensurabilidade existiu primeiro entre os números.” Proclus
“Como afirma Fowler, essa técnica teria sido usada para desenvolver uma teoria de razão independente da noção de proporção. Segundo o historiador, 3 noções distintas de razão estariam presentes na tradição grega: uma vinda da teoria musical; outra, da astronomia (que teria servido de base para as definições do livro V dos Elementos); e uma terceira, baseada na antifairese.”
“Se temos, por exemplo, um quadrado de lado 1, esse lado não é comensurável em comprimento com a diagonal. No entanto, seu quadrado 1 é comensurável com o quadrado da diagonal, que é 2. É lícito dizer, então, que essas grandezas são comensuráveis em potência.”
“as teses atuais sugerem que houve um desenvolvimento contínuo da matemática, e não uma ruptura, antes e depois do momento em que se percebeu a possibilidade de duas grandezas serem incomensuráveis.”
“Reza a lenda que a descoberta dos irracionais causou tanto escândalo entre os gregos que o pitagórico responsável por ela, Hípaso, foi expulso da escola e condenado à morte. Não se sabe de onde veio essa história, mas parece pouco provável que seja verídica. Em um artigo publicado em 1945, ‘The discovery of incommensurability by Hippasos of Metapontum’ (A descoberta da incomensurabilidade por Hípaso de Metaponto), Von Fritz conjectura que a incomensurabilidade tenha sido descoberta durante o estudo do problema das diagonais do pentágono regular, que constituem o famoso pentagrama. A lenda da descoberta dos irracionais por Hípaso foi erigida a partir desse exemplo. Entretanto, os historiadores que seguimos aqui contestam tal reconstrução, uma vez que ela implica o uso de fatos geométricos elaborados que só se tornaram conhecidos depois dos Elementos de Euclides.”
“Não sabemos exatamente qual a importância da geometria na escola pitagórica, mas acredita-se que não tenha sido tão relevante quanto a aritmética. Para os pitagóricos, que praticavam aritmética com números representados por pedrinhas e estavam preocupados com teorias sobre o cosmos, resumidas pelo enunciado <tudo é número>, a descoberta da incomensurabilidade não deve ter tido nenhuma importância. A teoria dos números desenvolvida por eles e a matemática abstrata, associada à geometria, estavam em dois planos distintos: <tudo é número> não significava <todas as grandezas são comensuráveis>.”
“A afirmação de que a descoberta da incomensurabilidade produziu uma crise nos fundamentos da matemática grega foi consolidada por trabalhos de historiadores da 1ª metade do século XX. P. Tannery já havia afirmado que tal descoberta significou um escândalo lógico na escola pitagórica do século V, sendo mantida em segredo inicialmente, até que, ao se tornar conhecida, teve como efeito desacreditar o uso das proporções na geometria. Um dos artigos mais influentes a propalar a ocorrência de uma crise foi ‘Die Grundlagenkrisis der griechischen Mathematik’ (A crise dos fundamentos da matemática grega), de Hasse & Scholz, publicado em 1928, que fazia referência somente à possibilidade de ter havido uma crise dos fundamentos da matemática grega.”
“O problema da incomensurabilidade parece ter surgido no seio da própria matemática, mais precisamente da geometria, sem a relevância filosófica que lhe é atribuída. Ao contrário da célebre lenda, os historiadores citados, como Burkert e Knorr, contestam até mesmo que essa descoberta tenha representado uma crise nos fundamentos da matemática grega. Não se encontra alusão a escândalo em nenhuma passagem dos escritos a que temos acesso e que citam o problema dos incomensuráveis, como os de Platão ou Aristóteles. Aristóteles, aliás, não cita o problema dos incomensuráveis nem mesmo em sua crítica aos pitagóricos.”
“Em ‘Impact of modern mathematics on ancient mathematics’ (Impacto da matemática moderna sobre a matemática antiga), Knorr interpreta as diferentes versões da crise dos incomensuráveis que dominaram a historiografia em meados do século XX como um sinal da influência de pressupostos filosóficos. Os estudos meta-matemáticos do período foram marcados pelo questionamento em relação aos fundamentos da matemática, associado aos trabalhos de Dedekind, Cantor e Hilbert. A tentação de ver nos gregos uma crise análoga era um modo de valorizar os trabalhos do início do século XX, encarados como soluções para dilemas não resolvidos por 2500 anos.”
“É provável que a antifairese entre o lado e a diagonal do quadrado fosse conhecida de modo geométrico nos séculos V e IV sem que se atribuísse ao procedimento o valor de uma demonstração da incomensurabilidade. Outra hipótese sobre a descoberta da incomensurabilidade, dessa vez no contexto da aritmética, tem sua origem em um resultado atribuído a Euclides. No final do século IV, Aristóteles se refere à prova da incomensurabilidade em sua exposição sobre a técnica de raciocínio por absurdo, dizendo que: se o lado e o diâmetro são considerados comensuráveis um em relação ao outro, pode-se deduzir que os números ímpares são iguais aos pares; essa contradição afirma, portanto, a incomensurabilidade das duas grandezas.” “Mas a demonstração desse fato faz uso de uma linguagem algébrica que não poderia ter sido usada pelos gregos antigos.” Ar., gênio, mas sempre menino bobo!
“Na matemática grega anterior a Euclides, os problemas geométricos eram tratados como se fossem cálculos com números. Foi justamente a descoberta dos incomensuráveis que provocou uma separação entre os universos das grandezas e dos números. A demonstração pré-euclidiana da incomensurabilidade não pode ter se servido, portanto, dessa separação. Logo, a prova encontrada nesse apêndice deve ser tardia e com certeza não foi por meio dela que se descobriu a incomensurabilidade.”
“Por volta do ano 375, Platão criticou os geômetras por não empregarem critérios de rigor desejáveis para as práticas matemáticas. Não por acaso o trabalho de Eudoxo se desenvolveu no seio da academia platônica. Sendo assim, ainda que não possamos dizer que a transformação dos fundamentos da matemática grega é devida a Platão, este expressa o descontentamento dos filósofos com os métodos adotados pela matemática e articula o trabalho dos pensadores à sua volta para que se dediquem a formalizar as técnicas utilizadas indiscriminadamente.”
“Temos notícia dos paradoxos de Zenão por fontes indiretas, como a Física de Aristóteles, e seus objetivos estão expostos no diálogo Parmênides de Platão. Tais paradoxos são mencionados algumas vezes em conexão com o problema dos incomensuráveis. No entanto, os argumentos de Zenão se voltam contra pressupostos filosóficos. Além disso, a descoberta da incomensurabilidade deve ter se dado depois da época de Zenão, o que nos leva a concluir que seus paradoxos nada têm a ver com a questão. Em livros de história da matemática, é comum também relacionar esses paradoxos ao desenvolvimento do cálculo infinitesimal e do conceito de limite. Trata-se, no entanto, de uma interpretação a posteriori.”
“O pensamento dos eleatas busca ultrapassar a percepção e fundamentar a filosofia em bases não-empíricas. A filosofia do Uno nega veementemente a possibilidade de que as coisas possam ser subdivididas, já que essa divisão implica a constituição de uma pluralidade. Zenão queria mostrar, com seus paradoxos, que é absurdo considerar não apenas que as coisas são infinitamente divisíveis, mas também que são compostas de infinitos indivisíveis. Os paradoxos dizem respeito à impossibilidade do movimento, no caso de admitirmos quaisquer dessas hipóteses. § Esses paradoxos contra o movimento só são conhecidos na forma exposta por Aristóteles, com o objetivo de refutá-los. Nenhum argumento matemático é usado em sua contestação.” Ainda o mesmo dos pseudo-divulgadores científicos de hoje: ‘Olha só, um físico afirmou que o tempo não existe!!’
“A série que pode ser usada para traduzir o problema de Zenão é ½ + (½)² + (½)³ cuja soma deve ser igual a 1.”
Demonstração moderna:
0,999999… = 0,9 + 0,09 + … = 9/10 + 9/100 + 9/1000 + … = 9/10 / (1 – 1/10) = ½ / (1 – ½) = 1
Resumindo todo o teor do capítulo:
A historiografia calibrada recente nos ensina que:
Pitágoras é o Pai da matemática indutiva grega;
Euclides é o Pai da matemática dedutiva grega. (Pai – conhecido! – da Axiomática)
“Por que então o método dedutivo teria sido empregado na matemática grega e quais as causas da adoção da noção de prova? § Problemas matemáticos complexos começaram a surgir por volta do quinto e quarto séculos, como o de expressar o comprimento da diagonal em termos do lado de um quadrado. Esse não era somente um problema ainda não-resolvido, era um problema que desafiava a percepção, além de não poder ser abordado somente por meio de cálculos. A lógica matemática e a prova dedutiva podem ir além do que é perceptível.”
“Por um lado, os matemáticos tinham de lidar com a complexidade e o caráter abstrato de alguns problemas que contradiziam a intuição e não eram acessíveis por meio de cálculos. Por outro, a organização em escolas, cujo objetivo era transmitir o conhecimento matemático da época, pode ter gerado uma demanda pela compilação e sistematização desse conhecimento. A necessidade de colocar em ordem a aritmética e a geometria herdadas das tradições mais antigas, bem como as descobertas recentes, deve ter levado, naturalmente, a um questionamento sobre a forma de expor o conteúdo matemático.”
Tudo que é abstrato se cimenta no ar.
“Uma das primeiras evidências diretas e extensas sobre a geometria grega no período aqui considerado, para além de fragmentos ou reconstruções tardias, é o diálogo platônico intitulado Mênon, que se supõe tenha sido escrito por volta do ano 385 a.C.” Minha tradução de trechos (os matemáticos sempre em verde): https://seclusao.art.blog/2020/01/22/menon-ou-da-virtude-ou-da-inexistencia-de-uma-ciencia-politica-ultima-traducao-do-ciclo-platao-obras-completas-virginia-woolf-ao-final/.
Sem que minha tradução fosse prejudicada por isso, fi-la da seguinte forma (linhas vermelhas), ao passo que Sócrates na verdade se referia às linhas cinzentas (acontece que essa era uma forma de demonstrar a incomensurabilidade da diagonal do quadrado numa forma bidimensional, enquanto que na minha tradução aludi ao cubo, tridimensional, em nota de rodapé):
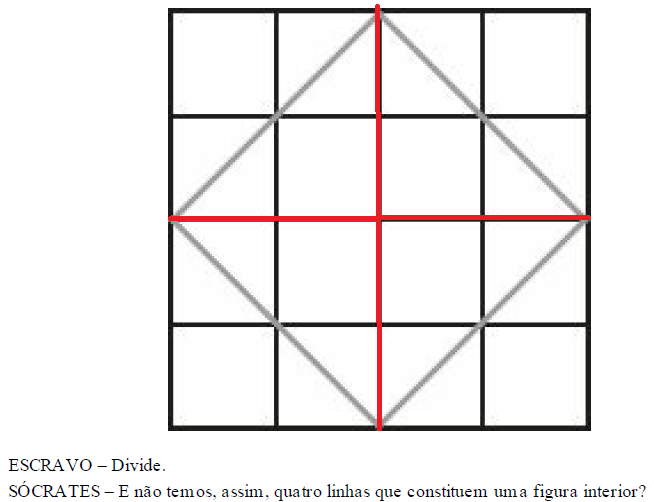
Com efeito, eis o quadrado de oito pés de área, a olho nu. A palavra diagonal não aparece no texto, apenas lado. Porque a diagonal é, afinal, um lado de outro quadrado, justaposto.
“A pergunta sobre quanto mede a diagonal não chega nem mesmo a ser evocada, talvez porque Sócrates saiba que essa medida não pode ser encontrada no universo dos números admitidos até então. Mas, além disso, talvez ele quisesse apresentar ao escravo um novo tipo de conhecimento, no qual basta exibir a linha sobre a qual o quadrado deve ser construído.”
Vemos que embora minha intenção fosse diferente da da autora (Tatiana Roque), não discordamos nada a respeito do diálogo (a evidenciação do conceito de reminiscência X o correto ensino da matemática geométrica, em que pese a ‘irracionalidade do número da diagonal’). É que em algum momento ambas as coisas são uma só na exposição de Sócrates. O que fica evidente no meu trecho comentado que reproduzo aqui: “Este raciocínio todo, bem simples, serve para lembrar, também: não é todo matemático que é bom em ensinar matemática. É preciso saber o método para não fazer o aluno <descobrir a natureza> da forma indesejada (pelo ensino oficial, pelos livros, pelo próprio educador, etc.). Mostrar que o jovem se equivocava ao imaginar o quadrado e que se daria conta do erro ao contar os quadrados após desenhar o quadrado na areia favorecia Sócrates na discussão que tinha com Mênon (sobre a teoria da reminiscência).” O que mostra, ainda, o quão visual era, àquela altura, a matemática para os gregos!
Mas continuando…
“A geometria, tal como a conhecemos atualmente, lida com formas abstratas. Um quadrado não é o quadrado que desenhamos no papel; é uma forma abstrata, a forma <quadrado>. Os objetos geométricos de base – como o ponto, a reta e o plano – também não são concretos. O ponto é algo sem dimensão, que não existe na realidade. Logo, esses objetos só podem ser concebidos por meio de uma abstração.” Parênteses filosóficos importantes: a idéia platônica é só isso: a verdade não está no fenômeno! Aristóteles, tão genial em suas sistematizações, não foi capaz de compreendê-lo. Ao contrário das aparências, não foi seu melhor aluno… Ou, não importa: enquanto aluno presencial, na Academia, talvez até tenha sido. Mas nós somos alunos muito melhores neste século! Em nenhum momento se tratava de criar duplos metafísicos, mas de descrever o Um parmenídeo.
O conhecimento não são sombras, mas também não é o sol ou qualquer imagem tridimensional fora da caverna (precaução contra a hiper-fenomenologia)…
“A matemática parte sempre de primeiros princípios: um conjunto de hipóteses a partir das quais se poderá descer até as conclusões, que constituirão o conhecimento científico. Nesse processo, objetos sensíveis se fazem necessários, o que é muito claro na matemática: raciocinar sobre um quadrado hipotético exige o emprego do desenho de um quadrado no quadro-negro, ainda que saibamos que esse quadrado desenhado não é o verdadeiro quadrado. A dialética é um conhecimento de tipo distinto, que usa as hipóteses como ponto de partida para um mundo acima delas, no qual não há hipóteses.” Nessa última frase serei obrigado a discordar: Platão nunca fez essa distinção. Todo transcender ao que está por trás das aparências, o verdadeiro, ainda é sempre um exercício de engatinhar e tatear por entre hipóteses…
“Entre as ciências hipotéticas, a geometria é o principal exemplo usado por Platão. Essa ciência utiliza hipóteses e dados sensíveis para chegar a conclusões de modo consistente. Um de seus traços distintivos é o fato de utilizar formas visíveis com o fim, somente, de investigar o absoluto que encerram. Quando um geômetra pesquisa as propriedades de um quadrado desenhado no quadro-negro – cópia do quadrado ideal –, é o verdadeiro quadrado que ele pretende simular e não meramente a sua cópia. As verdades da Idéia só podem ser vistas com os olhos do pensamento, e em sua busca a alma é obrigada a usar os primeiros princípios, descendendo destes suas conseqüências.” Agora se expressou melhor!
“A OBRA Elementos, de Euclides, é vista como o ápice do esforço de organização da geometria grega desenvolvida até o século III a.C. Por um lado, afirma-se que seria somente uma compilação de resultados já existentes produzidos por outros, o que torna o seu autor um mero editor. Por outro, celebra-se que esses trabalhos tenham sido expostos de um modo novo, o que revelaria a predominância na Grécia, nessa época, de um pensamento lógico e dedutivo.”
CAPÍTULO 3. Problemas, teoremas e demonstrações na geometria grega
“Os Elementos de Euclides são um conjunto de 13 livros publicados por volta do ano 300, mas não temos registros da obra original, somente versões e traduções tardias.”
“Do ponto de vista histórico, cabe perguntar até que ponto o padrão que esse livro exprime era realmente preponderante na matemática que se desenvolveu antes e depois de Euclides. Além disso, é fato, as construções propostas nessa obra são efetuadas por meio da régua e do compasso. Mas seria essa restrição decorrente de uma proibição de outros métodos de construção? Teria essa determinação afetado toda a geometria depois de Euclides?” “Um dos objetivos deste capítulo é relativizar a tese da influência platônica na reorganização da geometria, bem como o papel das técnicas de construção propostas nos Elementos no contexto das práticas gregas de resolução de problemas.”
“Todo enunciado universal sobre um objeto geométrico é um teorema geométrico. Os problemas são um primeiro passo para passarmos do mundo prático à geometria. (…) Grande parte da crença que temos na motivação platônica de Euclides decorre da utilização dos Comentários de Proclus. A Coleção matemática de Pappus é outra das principais fontes de conhecimento dos trabalhos matemáticos gregos, cujos registros originais se perderam.”
“A resolução de problemas geométricos envolve sempre uma construção, e o critério usado nessa classificação baseia-se nos tipos de linhas necessárias para efetuá-la. Além da régua e do compasso, são listados métodos que usam cônicas e curvas mecânicas, como a quadratriz, a espiral e o conchóide de Nicomedes, conhecidos antes do fim do século III. As construções com régua e compasso não permitem resolver todos os problemas propostos pelos matemáticos gregos antes e depois de Euclides, que não se furtavam, por isso, a utilizar outros métodos.”
“A visão de que os matemáticos gregos se aferravam aos fundamentos e a padrões rígidos tem origem na história da matemática desenvolvida na virada dos séculos XIX e XX, período marcado por pesquisas sobre o rigor da matemática dessa época. O objetivo dos trabalhos de Hilbert, por exemplo, era justamente fundamentar a geometria euclidiana. Mas será que os matemáticos da Antiguidade eram tão preocupados assim com questões de fundamento quanto os do final do século XIX?”
“Nos primeiros livros dos Elementos, muitos resultados parecem pertencer a uma tradição que podemos chamar de ‘cálculo de áreas’, que inclui a transformação de uma área em outra equivalente, bem como a soma de áreas. Veremos que as proposições dos livros I e II podem ser entendidas a partir dessas práticas, incluindo o teorema sobre a hipotenusa do triângulo retângulo,
dito ‘de Pitágoras’.”
“Arquimedes nasceu mais ou menos no momento em que Euclides morreu, em torno da segunda década do século III. Era de esperar, portanto, que o trabalho de Euclides tivesse uma influência marcante em sua obra. Mas não foi bem assim. Arquimedes não pode ser visto como sucessor de Euclides; e seu trabalho não se inscreve, por assim dizer, em uma tradição euclidiana. Um exemplo disso é a utilização de métodos mecânicos de construção, caso da espiral de Arquimedes.”
“Entre os diversos problemas matemáticos clássicos difundidos antes de Euclides estão o da duplicação do cubo (problema deliano) e o da quadratura do círculo.”
“Há diversas construções para as meias proporcionais que datam de períodos posteriores e podem ser encontradas em Três excursões pela história da matemática, de J.B. Pitombeira. Entre elas está a de Menecmo, que viveu por volta de 350 e foi aluno de Eudoxo. O seu conhecimento da teoria das razões e proporções permitia concluir, sem usar equações, que o ponto que satisfaz o problema das meias proporcionais é a interseção de duas cônicas, uma parábola e uma hipérbole, que atualmente seriam dadas, respectivamente, pelas equações y² = bx e xy = ab.”
“Por valorizar a matemática teórica, Platão teria desprezo pelas construções mecânicas, realizadas com ferramentas de verdade. A régua e o compasso, apesar de serem instrumentos de construção, podem ser representados, respectivamente, pela linha reta e pelo círculo, figuras geométricas com alto grau de perfeição.” “é coerente dizer que sua filosofia encarava a reta e o círculo como figuras geométricas superiores, mas também não há, em seus escritos, indicações explícitas de imposição dessas figuras como protótipos para toda a geometria, nem de proibição do uso de outras construções.”
OS CHATÕES DOS 1800! “O responsável por creditar a Platão a restrição à régua e ao compasso é o matemático alemão Hermann Hankel, que atuou na segunda metade do século XIX e trabalhou com matemáticos como Weierstrass e Kronecker, conhecidos pela preocupação com os fundamentos da matemática. Em 1874, Hankel publicou um texto histórico sobre a geometria euclidiana – Zur Geschichte der Mathematik in Alterthum und Mittelalter (Sobre a história da matemática na Idade Média e na Antiguidade) – contendo extrapolações com base em trechos da obra de Platão. Em uma tese meticulosa sobre o papel da restrição à régua e ao compasso escrita em 1936, mas que continua uma referência sobre o nascimento desse mito, o alemão A.D. Steele analisa por que a tese de Hankel é falsa e fornece algumas hipóteses sobre as razões do uso exclusivo desses instrumentos nos Elementos de Euclides. Referimo-nos especificamente aos Elementos, pois a restrição à régua e ao compasso não parece ser importante nem mesmo em outros escritos de Euclides.”
“Quer optemos pela motivação pedagógica ou por essa segunda razão, de cunho epistemológico, parece mais adequado entender a exclusividade da régua e do compasso nos Elementos como uma restrição pragmática cujo objetivo poderia ser apresentar um uso ótimo dos instrumentos mais simples possíveis.”
“O tipo de organização dos Elementos também é objeto de extensas pesquisas, pois os resultados dos primeiros livros não são necessariamente os mais antigos, ou seja, a obra não é organizada de modo cronológico. Acredita-se que os livros VII a IX – os livros aritméticos dos Elementos, atribuídos aos pitagóricos – sejam os mais antigos. Os livros II, III e IV não apresentam uma ordem seqüencial tão nítida quanto a dos livros I, V e VI, o que pode indicar que aqueles sejam anteriores a esses. Além disso, nos livros I a IV, as construções e provas são realizadas por métodos de congruência e pelo cálculo de áreas e não empregam razões e proporções, que já eram conhecidas muito antes de Euclides. Isso poderia ser um indício de que eles teriam sido escritos depois da descoberta dos incomensuráveis, que demandou uma nova teoria das razões e proporções. A partir desse momento, parece ter havido uma reorganização do conhecimento geométrico. A exposição de resultados envolvendo semelhança de figuras, por exemplo, que já eram bastante antigos, foi adiada para depois do livro V, uma vez que necessitava de uma teoria geral das razões e proporções para grandezas (incluindo as incomensuráveis).”
“Um traço particular dos Elementos é que as grandezas são tratadas enquanto tais e jamais são associadas a números (ao contrário, nos livros sobre números, eles são tratados como segmentos de reta).” “Alguns pesquisadores, como Fowler, afirmam que o livro V dos Elementos, que contém uma teoria das razões e proporções, trata de resultados mais recentes do que os outros livros.
Resumindo, podemos traçar a seguinte cronologia: os livros VII a IX, que seriam os mais antigos, empregam uma linguagem ingênua de razões e proporções que estaria presente desde épocas muito remotas, antes da descoberta dos incomensuráveis; os livros I a IV tratam de resultados sobre equivalência de áreas também antigos, mas as demonstrações evitam o uso de razões e proporções; no livro V é apresentada a nova teoria das razões e proporções, servindo de base para o estudo de equivalência de áreas e semelhança de figuras de um novo modo, o que é feito no livro VI. Além disso, o livro I teria sido escrito com o intuito de apresentar os princípios, por isso exibiria um cuidado especial com o encadeamento das proposições.”
“Uma definição é um tipo de hipótese da qual o aprendiz não tem uma noção evidente, mas faz uma concessão àquele que as ensina e aceita-a sem demonstração. As definições que iniciam os Elementos fazem referência aos objetos matemáticos que serão utilizados ao longo da obra e que possuem um conteúdo intuitivo.”
“Livro I – Definições
1. Ponto é aquilo de que nada é parte
2. E linha é comprimento sem largura
3. E extremidades de uma linha são pontos
4. E linha reta é a que está posta por igual com os pontos sobre si mesma
5. E superfície é aquilo que tem somente comprimento e largura
6. E extremidades de uma superfície são retas
…
10. E quando uma reta, tendo sido alteada sobre uma reta, faça os ângulos adjacentes iguais, cada um dos ângulos é reto, e a reta que se alteou é chamada uma perpendicular àquela sobre a qual se alteou
…
15. Círculo é uma figura plana contida por uma linha (que é chamada circunferência), em relação à qual todas as retas que a encontram (até a circunferência do círculo), a partir de um ponto dos postos no interior da figura, são iguais entre si
…”
“Na definição 4, o termo linha reta designa o que hoje chamamos de segmento de reta. À maneira de Euclides, usaremos aqui o termo reta com esse sentido.” “A definição 15 está na origem da distinção entre círculo e circunferência encontrada em alguns livros-texto atuais.”
“Uma noção comum, segundo Proclus, é um enunciado de conteúdo óbvio, tido facilmente como válido pelo aprendiz. Se além de o enunciado ser desconhecido ele é proposto como verdadeiro por meio de alguma argumentação temos um postulado. Nesse caso, é necessário que aquele que ensina convença o aprendiz de sua validade.”
“Livro I – Postulados
1. Fique postulado traçar uma reta a partir de todo ponto até todo ponto
2. Também prolongar uma reta limitada, continuamente, sobre uma reta
3. E, com todo centro e distância, descrever um círculo
4. E serem iguais entre si todos os ângulos retos
5. E, caso uma reta, caindo sobre duas retas, faça os ângulos interiores e do mesmo lado menores do que dois retos, sendo prolongadas as duas retas, ilimitadamente, encontrarem-se no lado no qual estão os menores do que dois retos
Livro I – Noções comuns
1. As coisas iguais à mesma coisa são também iguais entre si
2. E, caso sejam adicionadas coisas iguais a coisas iguais, os todos são iguais
3. E, caso de iguais sejam subtraídas iguais, as restantes são iguais
4. E, caso iguais sejam adicionadas a desiguais, os todos são desiguais
…
8. E o todo é maior do que a parte
9. E duas retas não contêm uma área”
“Os enunciados da matemática seguem-se, por demonstração, dos primeiros princípios. Essa é a definição do método axiomático-dedutivo. Mas por que Euclides usou esse método?”
“Como vimos, o objetivo da proposição I-45 é mostrar como se pode construir um paralelogramo, com ângulo dado, cuja área seja igual à de um polígono qualquer. Observemos que essa construção torna possível representar a área de qualquer polígono como um retângulo, uma vez que o retângulo é um caso particular de paralelogramo, com ângulos retos. Para entender a importância dessa construção, é preciso saber como eram realizados os cálculos de áreas na geometria grega.
Atualmente, medir é associar uma grandeza a um número. Se quisermos somar as áreas de dois polígonos, teremos de calcular a área de cada um, por meio de uma fórmula, e somar os resultados (que são números). Mas nesse momento as grandezas não eram tratadas por meio de associação a números.”
“para ‘medir’ a área de uma figura qualquer, deveríamos encontrar uma figura simples cuja área fosse igual à da figura dada. Essa figura simples era um quadrado. Logo, o problema de encontrar a quadratura de uma figura qualquer era equivalente ao problema de construir um quadrado cuja área fosse igual à da figura dada.”
“Os primeiros princípios servem, portanto, à demonstração dos primeiros resultados, que, em seguida, efetuarão o papel de premissas para novas demonstrações. O encadeamento dedutivo das proposições pode ser compreendido, assim, como a busca de uma espécie de economia na argumentação.”
“se 2 triângulos têm 2 lados iguais e os ângulos formados por eles também iguais, então os triângulos são congruentes. O uso do termo ‘congruente’ é bem mais recente e tem como objetivo resolver uma inconsistência lógica colocada pela formalização posterior da geometria euclidiana. Na lógica, o princípio da identidade afirma que uma coisa só é igual a si mesma. Portanto, 2 triângulos ou 2 figuras geométricas quaisquer não podem ser iguais. Daí o emprego do termo ‘congruente’, que significa, intuitivamente, que 2 figuras podem ser colocadas uma em cima da outra.” A lógica não é sempre lógica.
“se 2 triângulos ABC e DBC possuem a mesma base e o terceiro vértice em uma paralela à base, então eles têm áreas iguais. Atualmente, dizemos que 2 triângulos têm áreas iguais se possuem a mesma base e a mesma altura, uma vez que a área é calculada pela fórmula bh/2.Como tratamos aqui de uma tradição geométrica que não associava grandezas a números, não se mediam a base e a altura para calcular a área. A proposição I-38 procura dizer em que casos duas áreas são equivalentes sem que seja preciso calculá-las. Ora, se o 3º vértice de 2 triângulos está em uma paralela à base, eles possuem as mesmas alturas. Como é dado que as bases são iguais, eles têm também a mesma área. As 2 últimas proposições do livro I são justamente o resultado conhecido como teorema ‘de Pitágoras’ e o seu recíproco.”
“Proposição I-47
Nos triângulos retângulos, o quadrado sobre o lado que se estende sob o ângulo reto é igual aos quadrados sobre os lados que contêm o ângulo reto. [mal-redigido pra porra, como veremos mais abaixo!]
Demonstração: Seja o triângulo retângulo ABC, com ângulo reto BAC. Queremos mostrar que a área do quadrado construído sobre o lado BC é igual à soma das áreas dos quadrados construídos sobre os lados AB e AC, que formam o ângulo reto BAC. Vamos ilustrar a demonstração com figuras que não foram usadas por Euclides, [não fosse isso e dificilmente entenderíamos] mas manteremos o espírito de sua prova. Descrevemos sobre cada lado um quadrado e vamos mostrar que a área do quadrado construído sobre o lado BC pode ser obtida pela soma de 2 retângulos, um deles com área igual à do quadrado construído sobre AB (em cor branca na Ilustração 10) e o outro com área igual à do quadrado construído sobre AC (de cor cinza).
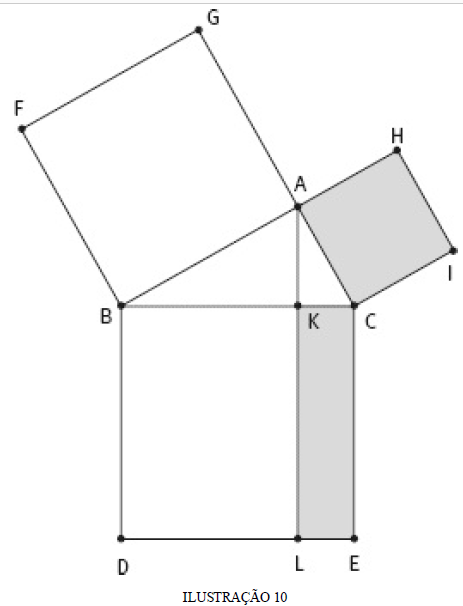
“Queremos mostrar que a área do quadrado ABFG é igual à do retângulo BDLK. Os próximos passos para concluir essa demonstração são os seguintes:
1. Mostrar que a área do triângulo ABF, que é metade do quadrado ABFG, é igual à área do triângulo DBK, que é metade da do retângulo BDLK.
2. Para isso, mostraremos que a área de ABF é igual à de CBF e que a área de DBK é igual à de ABD.
3. Como já mostramos que a área de ABD e de CBF são iguais, concluiremos que a área de ABF é igual à área de DBK, assim, a área do quadrado ABFG será igual à do retângulo BDLK.
Como os ângulos BAC e BAG são retos, os segmentos CA e AG estão sobre uma mesma reta. Como essa reta é paralela a BF, temos que CBF e ABF são triângulos de mesma base com o 3º vértice em uma paralela a essa base. Logo, pela proposição I-38, eles possuem a mesma área. De modo análogo, como AL foi construída paralelamente a BD, temos que ABD e DBK são triângulos de mesma base com 3º vértice em uma paralela à base, sendo assim, possuem a mesma área. Esse parágrafo, juntamente com o anterior, conclui a etapa 2.”
“Encontrar a ‘quadratura’ significava, no contexto grego, achar a área de uma figura dada. Usando essa proposição, como seria possível, portanto, comparar as áreas de dois retângulos sem calculá-las? Basta construir os quadrados com áreas iguais às dos retângulos e comparar os lados. E como podemos somar as áreas de dois retângulos? Basta construir os quadrados com áreas iguais às dos retângulos e somar as áreas desses quadrados por meio do teorema ‘de Pitágoras’.”
“Em grego, a palavra ‘hipérbole’ refere-se ao fato de que a base do paralelogramo resultante excede o segmento dado, ou seja, a figura construída possui como excesso a figura semelhante ao paralelogramo dado. ‘Hiperbólico’ remete a excessivo. Quando, inversamente, fica faltando uma figura para completar o segmento dado, tem-se uma situação associada a ‘elipse’. O paralelogramo pedido é construído de modo que fique faltando uma figura semelhante à figura dada, e a palavra ‘elíptico’ quer dizer que algo está faltando.” “Nesse caso, em que não há nenhuma figura excedendo a construção pedida, o paralelogramo é construído exatamente sobre o segmento. A origem da palavra ‘parábola’, em grego, remete ao fato de a figura ser construída de modo exato. As cônicas que conhecemos como parábola, hipérbole e elipse ganharam tais nomes no trabalho de Apolônio, justamente porque são usados métodos de aplicação de áreas em suas construções.”
“Vimos que enunciados dos Elementos de Euclides possuem um estilo geométrico. Seus problemas e teoremas têm um caráter essencialmente geométrico e devem ser demonstrados para as figuras empregadas consideradas do modo mais geral possível, ou seja, sem associar suas dimensões a medidas precisas. Apesar dessa evidência, entre o final do século XIX e meados do XX, matemáticos e historiadores, como H. Zeuthen e B.L. van der Waerden, postularam que as proposições do livro II dos Elementos seriam, na verdade, propriedades algébricas enunciadas sob uma roupagem geométrica. Por essa razão, os resultados desse livro são freqüentemente denominados ‘álgebra geométrica’. Esses pesquisadores se baseavam na hipótese de que as proposições do livro II são formulações geométricas de regras algébricas, como as que permitem resolver uma equação do 2º grau.”
“Em 1975, o romeno Sabetai Unguru escreveu um artigo atacando os defensores da tese da ‘álgebra geométrica’ e ressaltando que ler os textos gregos com a matemática moderna em mente pode nos fazer esquecer que aqueles se baseavam em pressupostos próprios. A partir daí, instaurou-se uma querela acirrada em torno da álgebra geométrica e da natureza da matemática euclidiana. Matemáticos historiadores, como André Weil e Hans Freudenthal, uniram-se contra os argumentos de Unguru, que passou a ser marginalizado pelas revistas mais importantes da época. A discussão9 teve consequências metodológicas importantes, ainda que não imediatamente, pois os historiadores se conscientizaram de que pode não ser conveniente traduzir os textos geométricos gregos em linguagem algébrica, como Heath havia feito com os Elementos de Euclides e Neugebauer com as Cônicas de Apolônio. Por essa razão, S. Unguru é reconhecido atualmente como um dos pioneiros nas transformações pelas quais a historiografia da matemática vem passando.
O ponto de vista algébrico mascara, por exemplo, uma singularidade essencial do tipo de argumentação usado na geometria grega: seu caráter sintético. Ou seja, a exposição analítica e algébrica que usamos hoje permite enunciar situações gerais, tratando os exemplos como casos particulares; no entanto, a geometria euclidiana não lidava com a generalidade de seus enunciados do mesmo modo. E, sobretudo, partia de premissas dadas e ia deduzindo os resultados passo a passo, a partir de conseqüências dedutíveis desses primeiros princípios.”
“Afora isso, as transformações de áreas operadas nos Elementos podem ser associadas às operações de adição, multiplicação e extração de raiz quadrada, mas nada indica que tais operações pudessem ser abstraídas das formas geométricas propriamente ditas.”
“Nos Elementos, o tratamento dos números (arithmos) é separado do tratamento das grandezas (mégéthos). Tanto as grandezas quanto os números são simbolizados por segmentos de reta. No entanto, os números são agrupamentos de unidades que não são divisíveis; já as grandezas geométricas são divisíveis em partes da mesma natureza (uma linha é dividida em linhas; uma superfície, em superfícies, etc.). A medida está presente nos 2 casos, mas mesmo quando uma proposição sobre medida possui enunciados semelhantes para números e grandezas, ela é demonstrada de modos distintos. As primeiras definições do livro VII apresentam a noção de número e o papel da medida.”
“Definição VII-3
Um número é uma parte de um número, o menor, do maior, quando meça exatamente o maior.
Essa última definição postula que um número menor é uma parte de outro número maior quando pode medi-lo, ou seja, os números são considerados segmentos de reta com medida inteira. Por exemplo, um segmento de tamanho 2 não seria parte de um segmento de tamanho 3, mas sim de um segmento de tamanho 6. Os números servem para contar, mas antes de contar é preciso saber qual a unidade de contagem.”
“A ‘unidade’, na definição de Euclides, é o que possibilita a medida, mas não é um número. Sendo assim, é inconcebível que a unidade possa ser subdividida.”
“É (…) com razão que o Uno não é considerado um número, pois a unidade de medida não é uma pluralidade de medidas.” Ar., Metafísica
DEFINIÇÃO DO MÁXIMO DIVISOR COMUM
“Proposição VII-1
Sendo expostos dois números desiguais, e sendo sempre subtraído de novo o menor do maior, caso o que restou nunca meça exatamente o antes dele mesmo, até que reste uma unidade, os números do princípio serão primos entre si.
Proposição VII-2
Sendo dados dois números não primos entre si, achar a maior medida comum deles.”
“A proposição VII-1 fornece um critério para decidir quando dois números A e B são primos entre si. Supondo B < A, retira-se B de A obtendo-se um resto, R1. Se R1 não for igual a B, retira-se R1 de B, obtendo-se outro resto, R2. O procedimento continua enquanto nenhum dos restos sucessivos R1, R2,… for igual ao anterior e nem igual a 1. Quando um resto coincidir com o anterior, a próxima subtração resultará em 0 e os números A e B terão uma medida comum. Então a proposição VII-2 se aplica. Caso contrário, o resto será igual a 1 em alguma iteração e poderemos dizer que A e B são primos entre si. Na verdade, ao enunciar essa proposição 2 do livro VII, Euclides emprega uma linguagem de grandezas. Os dois números dados são os segmentos A e B dos quais queremos encontrar a maior medida comum.”
“Exemplo:
Como encontrar por este método o mdc de 119 e 85.
Solução:
Começo por retirar 85 uma vez de 119, obtendo R1 = 34 como resto. Em seguida, retiro 34 duas vezes de 85, obtendo o segundo resto, R2 = 17. Agora retiro 17 duas vezes de 34, obtendo 0. Logo, 17 é o maior divisor de 119 e 85. Note que, se fossem primos, esse procedimento chegaria ao resto 1, e não a 0.”
“Um número é primo quando não é medido por nenhum número, somente por 1, que não é considerado número.”
“Há, portanto, uma analogia entre grandezas incomensuráveis e números primos entre si. Só que a antifairese para números termina dando 1, ao passo que o mesmo procedimento aplicado a grandezas não termina no caso incomensurável, conforme visto no Capítulo 2 ao mostrarmos a incomensurabilidade entre o lado e a diagonal do quadrado.”
A FRAÇÃO AINDA NÃO NASCEU: “A terminologia mais empregada é a de que duas coisas ‘estão uma para a outra assim como’. Temos um exemplo disso na proposição 1 do livro VI: ‘Triângulos, e paralelogramos, com a mesma altura estão um para o outro assim como suas bases’.”
“Uma das motivações de Eudoxo pode ter sido aprimorar os procedimentos infinitos usados por Hipócrates em sua medida do círculo. O uso de processos que tendem ao infinito será efetuado por Arquimedes, usando seqüências de aproximações finitas da área do círculo por polígonos. A teoria das proporções de Eudoxo teria como objetivo enunciar teoremas gerais sobre proporções que valessem também para grandezas incomensuráveis, ou seja, que generalizassem os resultados obtidos por matemáticos mais antigos, como Hipócrates, Arquitas e Teeteto.”
“Definição V-5
Magnitudes são ditas estar na mesma razão, uma primeira para uma segunda e uma terceira para uma quarta, quando os mesmos múltiplos da primeira e da terceira ou, ao mesmo tempo, excedam, ou, ao mesmo tempo, sejam iguais, ou, ao mesmo tempo, sejam inferiores aos mesmos múltiplos da segunda e da quarta, relativamente a qualquer tipo que seja de multiplicação, cada um de cada um, tendo sido tomados correspondentes.”
“A definição 3 deixa claro que o conceito de razão é aplicado a grandezas homogêneas. Assim, importa observar a natureza da grandeza, não podendo haver razão entre um comprimento e uma área. Ainda que a razão diga respeito à quantidade, ela não será sempre calculável como um número.”
“Em outras palavras, a/b para os gregos não era um número. Sendo assim, nosso método não pode ser usado. Ou seja, para comparar a/b a c/d não é possível usar o argumento de que a/b = c/d se e somente se ad = bc.”
“Arquimedes é um dos matemáticos mais conhecidos do período pós-euclidiano. Seus livros possuem uma estrutura bastante distinta daquela que caracteriza os Elementos de Euclides e seus métodos não reproduzem o padrão euclidiano. Não se percebe em seus trabalhos uma preocupação nem em usar nem em defender um método de tipo axiomático, e a forma como expõe seus resultados não parece ter sofrido influência do estilo dos Elementos. Sem se restringir a nenhuma determinação a priori, Arquimedes usa métodos não-euclidianos, como a neusis, mesmo quando uma construção com régua e compasso é viável. Conforme sugere Knorr, ao invés de estender ou generalizar a estrutura axiomática da matemática, Arquimedes parecia estar mais preocupado em comunicar novas descobertas relativas à resolução de problemas geométricos.”
“No início de sua obra intitulada Quadratura da parábola, em uma carta a Dositheus, Arquimedes afirma que pretende comunicar ‘um certo teorema geométrico que não foi investigado antes e que foi agora investigado por mim e que eu descobri, primeiramente, por meio da mecânica, e que foi exibido, em seguida, por meio da geometria’. Esse tipo de procedimento fica ainda mais claro no livro O método dos teoremas mecânicos, encontrado apenas em 1899 e escrito para Eratóstenes” “Uma análise desse trabalho pode ser encontrada em S. Costa, ‘O método de Arquimedes’.”
“Em seus estudos sobre os trabalhos de Arquimedes, Knorr aventa a hipótese de que, no lugar de contribuir para o progresso da matemática, a ênfase no formalismo parecia distrair os geômetras do que realmente importava. A comunidade dos pensadores alexandrinos, que se formou no período pós-euclidiano, estava mais interessada em criticar detalhes das demonstrações do que em fornecer novos resultados, o que será abordado no Capítulo 4. Em diversas ocasiões, Arquimedes manifestou, de modo sutil, sua impaciência com esses formalistas que influenciaram a história da geometria grega.”
“A partir dessa definição, temos que a espiral é uma curva gerada por um ponto que se move sobre um segmento de reta com velocidade constante ao mesmo tempo em que esse segmento de reta se move, também com velocidade constante, circularmente, com uma extremidade fixa e a outra sobre uma circunferência.
A principal propriedade da espiral, que é bastante útil para problemas de construção, reside em associar uma razão entre arcos (ou ângulos) a uma razão entre segmentos. A espiral estabelece uma proporcionalidade entre uma distância em linha reta e uma medida angular, o que permite reduzir o problema de seccionar um ângulo ao problema mais simples de seccionar um segmento de reta. A distância entre a origem e um ponto sobre a espiral é proporcional ao ângulo formado pela reta inicial e pela reta que compõe esse ângulo. Essa é exatamente a propriedade expressa, em linguagem atual, pela equação polar da espiral, que pode ser escrita na forma r = aθ, θ ≥ 0.”
“Como mencionado, dividir um ângulo em 3 partes iguais era um dos problemas mais importantes da geometria grega. Sabemos dividir um ângulo em 2 partes iguais com régua e compasso, mas muitas foram as tentativas frustradas de encontrar um procedimento análogo para a trissecção do ângulo. Uma das motivações da espiral de Arquimedes é justamente apresentar uma solução para este problema”
“No século XVII, esse tipo de procedimento ficou conhecido como método da exaustão. Essa nomenclatura, no entanto, não é a mais adequada, uma vez que o método se baseia justamente no fato de que o infinito não pode ser levado à exaustão, isto é, não admite ser exaurido – pois por mais que nos aproximemos, nunca chegamos até ele. Analisaremos, em seguida, o modo como Arquimedes ‘calculava’ a área de um círculo na primeira proposição de um de seus livros mais antigos: Medida do círculo. ‘Calcular’ está entre aspas porque essa proposição é uma maneira de determinar a área do círculo encontrando uma figura retilínea, um triângulo, no caso, cuja área seja igual à área do círculo. Esse foi um dos resultados mais populares de Arquimedes em sua época, e o procedimento é análogo ao empregado na proposição XII-2 dos Elementos de Euclides, atribuída a Eudoxo.”
“O final do século III foi o período de maior popularidade dos 3 problemas clássicos (quadratura do círculo, duplicação do cubo e trissecção do ângulo). Esses problemas constituem o ponto comum dos trabalhos de diversos geômetras da época, como Eratóstenes, Nicomedes, Hípias, Diocles, Dionysodorus, Perseus e Zenodorus. Apesar de a maioria das fontes que continham esses trabalhos não ter sido preservada, há evidências de aplicações da geometria a problemas de astronomia, ótica, geografia e mecânica. Além disso, esses geômetras parecem ter sofrido influência direta de Arquimedes, o que pode ser constatado pelo uso de métodos mecânicos, como a espiral (e outras curvas geradas por movimentos mecânicos), e de diversos tipos de neusis. Contudo, nota-se também que eles se distanciaram um pouco do estilo de Arquimedes, uma vez que se dedicaram à procura de métodos alternativos em suas construções, indicando uma possível necessidade de ir além dos procedimentos disponíveis na época.”
“Para aqueles que desejam se aprofundar nas Cônicas de Apolônio [considerado o mais literal sucessor de Euclides], Fried & Unguru fornecem, em Apollonius of Perga’s Conica: Text, Context, Subtext. Mnemosyne Supplement., uma nova tradução desse texto, livre dos anacronismos que o associavam à suposta álgebra geométrica dos gregos.”
“Apolônio segue o estilo formal dos Elementos até nos detalhes do enunciado de certas proposições. Seus resultados parecem exprimir a tentativa de estender e tornar rigorosos os métodos antigos empregados no estudo de cônicas, desenvolvidos por Euclides (em sua obra sobre as cônicas) e Arquimedes. Uma das preocupações de Apolônio era apresentar soluções por meio de cônicas para os problemas clássicos, como a duplicação do cubo e a trissecção do ângulo, a fim de eliminar as soluções por neuses e por curvas especiais usadas por Arquimedes e outros.
A diversidade de métodos utilizados na resolução de problemas geométricos até o século III revela que, até esse estágio do desenvolvimento da matemática, o importante era resolver os problemas por qualquer técnica disponível. Esse Leitmotiv marcou a tradição grega de resolução de problemas geométricos.” “Os métodos de resolução de problemas utilizados por Euclides foram consolidados por Apolônio no período seguinte, ao passo que os procedimentos de Arquimedes só encontrariam seguidores bem mais tarde, por volta dos séculos XVI e XVII.”
“Os escritos da época helenística, como os de Arquimedes, Fílon, Diocles e Apolônio, são precedidos por prefácios esclarecedores para a história da matemática. O texto propriamente dito tende a ser ordenado por meio de definições e axiomas, a partir dos quais os teoremas se encadeiam dedutivamente. Esse tipo de exposição não dá lugar a comentários heurísticos sobre como e para quê aqueles resultados foram obtidos.”
“O início do século II a.C. foi marcado por um declínio na atenção dos matemáticos aos problemas geométricos avançados, o que não representou uma decadência do campo matemático e sim um deslocamento de interesse em direção a outras áreas, como a trigonometria e os métodos numéricos. Devido à influência desses métodos nos trabalhos desenvolvidos pelos árabes durante a Idade Média, eles serão abordados no Capítulo 4, quando trataremos desse período histórico.
W. Knorr tacha a escola de Alexandria, nos tempos de Arquimedes, de ‘academicista’. Mesmo a composição dos Elementos de Euclides, para ele, se relaciona aos ideais da época e, sobretudo, aos seus objetivos pedagógicos. Essa abordagem privilegiava uma exposição sintética, tornando inacessível o procedimento heurístico da descoberta e menosprezando toda consideração concreta ou prática. Knorr contrasta essa tendência com outras obras alexandrinas mais tardias, como as Métricas, de Heron, o Almagesto, de Ptolomeu, e a Aritmética, de Diofanto. Em Métricas, Heron fornece regras aritméticas para computar áreas de diferentes tipos de figuras planas. Ao contrário dessa orientação pedagógica, a exposição de Euclides não dá nenhuma pista sobre a aplicação de seus teoremas a problemas práticos. A abordagem teórica, de inspiração euclidiana, seria característica do ensino nas escolas filosóficas, pois o estudante deveria aprender matemática por meio da contemplação e não pela prática.”
“A visão de que os teoremas são superiores aos problemas tem origem em uma tradição bem posterior, conhecida atualmente por meio dos Comentários de Proclus, que datam do nosso século V.”
“NOS LIVROS DE HISTÓRIA DA MATEMÁTICA é comum encontrarmos, depois da explanação das mais importantes contribuições gregas, referências a autores isolados, como Heron, Ptolomeu ou Diofanto. Em seguida, faz-se uma breve descrição da prática matemática em ‘outras culturas’, como China e Índia, passando superficialmente pelos estudos dos árabes. Em livros mais antigos, a referência ao período chega a ser depreciativa, como em The Development of Mathematics (O desenvolvimento da matemática), de E.T. Bell, dos anos 1940. Ao capítulo sobre a geometria grega, dedicado à época na qual a matemática foi ‘firmemente estabelecida’, seguem-se dois curtos capítulos: ‘A Depressão européia’ e ‘Desvio pela Índia, Arábia e Espanha’. Em tempos recentes, não é comum cometer esses exageros, ainda assim as matemáticas chinesa, indiana e árabe são tratadas como exceções, em uma linha não diretamente relacionada à matemática teórica que nos foi legada pelos gregos.” Outras matemáticas me interessam…
“Os árabes, por exemplo, são reconhecidos sobretudo como tradutores da matemática grega e transmissores dessa tradição na Europa, possibilitando que as obras gregas chegassem ao Ocidente e fossem vertidas para o latim no final da Idade Média. O período do Renascimento teria podido, assim, desfrutar a influência grega e dar os primeiros passos em direção ao desenvolvimento da matemática como a conhecemos hoje. A história desse período de transição entre a matemática grega, de tipo axiomático, e o desenvolvimento da álgebra na Europa, entre os séculos XIV e XVI, é uma peça-chave na construção da tese de que nossa matemática é a legítima herdeira dos padrões gregos. A superioridade do caráter dedutivo dos Elementos de Euclides é reforçada pelo discurso sobre a suposta natureza prática da matemática na Antiguidade tardia e na Idade Média.”
CAPÍTULO 4. Revisitando a separação entre teoria e prática: Antiguidade e Idade Média
“entre as práticas transmitidas pelos árabes as mais valorizadas por esses historiadores são justamente aquelas que traduzem o ideal grego. As artes práticas e a mecânica têm um papel inferior.
À luz dos recentes questionamentos historiográficos, não podemos deixar de achar estranho o gigantesco salto, recorrente nos livros de história da matemática, registrado entre o século III a.C., quando viveu Euclides, e o século XV, quando a matemática voltou a se desenvolver na Europa. A ideia aqui é contribuir para a desconstrução de alguns mitos em torno do pensamento medieval, sobretudo aqueles que levaram à sua designação como <idade das trevas>.
Dentre os matemáticos árabes, o mais famoso é Al-Khwarizmi, do século IX, importante personagem no desenvolvimento da álgebra. Tal afirmação pode soar estranha, pois se o papel dos árabes foi essencialmente transmitir a matemática grega, conforme nos ensina a história tradicional, e se esta era marcada pela geometria, como eles podiam ter conhecimentos algébricos significativos?
Os escritos árabes foram, de fato, influenciados por suas traduções de obras gregas. No entanto, não devem ser reconhecidos somente por terem disseminado a matemática praticada na Grécia antiga. Dentre suas contribuições destacam-se pontos importantes que vão além do que hoje chamamos de álgebra, abrangendo também a geometria, a astronomia e a trigonometria. Ver J.L. Berggren, Episodes in the Mathematics of Medieval Islam. Contrapondo-se à tendência eurocentrista da visão tradicional, alguns historiadores mais recentes acabaram exagerando para o outro lado, ao defenderem que a matemática medieval do período islâmico já apresentava um desenvolvimento comparável ao da matemática moderna. Em suma, a questão é complexa e controvertida. Não sabemos sequer se é legítimo falar de ‘matemática árabe’, ou se é melhor designar as contribuições desse período como ‘islâmicas’, uma vez que nem todos os países dominados pelo Islã eram árabes. Sendo assim, para evitar confusão, quando empregarmos aqui o termo ‘matemática árabe’ estaremos nos referindo à matemática escrita em árabe.”
“A necessidade de abordar a divisão entre teoria e prática e de analisar o papel dessa cisão no desenvolvimento da matemática exige que nos debrucemos mais sobre o contexto social e político da época. Sendo assim, considerações sobre história geral estarão mais presentes neste capítulo do que nos outros.”
“O início da Idade Média tem sido tradicionalmente delimitado pela desintegração do império romano no Ocidente, no ano 476. A história desses eventos se mistura com a questão da fé religiosa, como se a racionalidade fosse uma conquista dos tempos posteriores ao Renascimento, conhecidos como a Idade da Razão. Mas que racionalidades existiram na Idade Média?
“A concepção de que as artes práticas e a mecânica eram o ‘patinho feio’ da ciência grega contradiz as lendas que exaltam as invenções de um dos maiores matemáticos gregos, Arquimedes, relacionando-o a descobertas mecânicas. Ver Plutarco, The Life of Marcellus, p.471.”
“Plutarco prossegue, citando as origens da mecânica, com Eudoxo e Arquitas, e mostrando que Platão investiu contra eles acusando-os de corruptores e destruidores da pura excelência da geometria, que deveria se ocupar somente de coisas abstratas. E finaliza, defendendo a importância da separação entre mecânica e geometria: ‘Por essa razão a mecânica foi tornada inteiramente distinta da geometria, e tendo sido durante um longo tempo ignorada pelos filósofos, acabou sendo vista como uma das artes militares.’” Novamente eu me pergunto: podemos confiar em Plutarco?
“É freqüente encontrarmos referência a Arquimedes como um grande mecânico, mas essa imagem foi construída a posteriori, e não sabemos bem o que Arquimedes pensava da mecânica, nem se via as próprias obras como voltadas para a mecânica. O fato é que, a partir do século I, vários autores de mecânica, ligados às instituições alexandrinas, citam Arquimedes como um dos maiores mecânicos gregos. Isso mostra que não podemos traçar um panorama do pensamento do século I usando o testemunho de uma só fonte, por exemplo, Plutarco,¹ nem tampouco identificar suas correntes hegemônicas.
¹ Anedotas como a que relata que Arquimedes desvendou o mistério da coroa do rei Hieron são hoje tidas como lendas, construídas por meio de testemunhos duvidosos em escritos de terceiros.” O famoso ‘um amigo de um amigo me contou…’, mas mais gourmet!
“No Dictionary of Scientific Biography (Dicionário de biografias científicas) organizado por C.C. Gillispie lemos que Heron era um homem educado e um matemático aplicado, engenhoso. No entanto, é reconhecido somente por suas preocupações pedagógicas e pela ligação que estabeleceu entre as práticas matemáticas dos babilônios e as desenvolvidas pelos árabes e pelos renascentistas europeus.
C. Boyer afirma que existiam 2 níveis de matemática na Antiguidade, uma de tipo clássico, eminentemente racional, conhecida como geometria, e outra mais prática, mais bem-descrita como geodésia, herdada dos babilônios e mencionada nos escritos de Heron. Esses níveis são apresentados como um testemunho da oposição entre teoria e prática, sendo a segunda menos valorizada que a primeira.”
“Passaremos em seguida à história da álgebra, cuja origem é freqüentemente associada aos métodos propostos por Diofanto, por volta do século III a.C. Sua contribuição é vista, no entanto, como exceção no contexto decadente da matemática alexandrina, já sob o domínio romano.”
“Preferiríamos, sem dúvida, falar de todas as práticas do período que podem ser chamadas de ‘matemáticas’. No entanto, para atingir nosso objetivo de relativizar a separação entre teoria e prática, escolhemos as manifestações que foram designadas como ‘algébricas’ pela história tradicional, uma vez que nos relatos desse tipo elas foram associadas a contextos ‘práticos’. Esses desenvolvimentos estão em íntima relação com a formulação do mito da matemática greco-européia. Em 1569, Petrus Ramus formulou claramente o mito em uma carta para Catarina de Médici, buscando persuadi-la a incentivar o trabalho dos matemáticos. Ele se refere à Europa como uma totalidade, acrescentando que a França seria a maior beneficiária do programa. Para muitos pensadores da época, somente os gregos e os europeus teriam dado contribuições valiosas à matemática, forjada como um saber eminentemente europeu. A obra matemática de Ramus não continha nada além do conhecimento dos árabes.
Contudo, a imagem da matemática expressa por ele foi reforçada, em seguida, por outras contribuições que produziram, de fato, novas abordagens e formalismos para erigir um conhecimento inspirado nos ideais gregos. Para se demarcar em relação a seus predecessores, François Viète, considerado um dos inventores da álgebra moderna, afirma ter fundado uma nova arte: a arte analítica.”
“O passo decisivo para a constituição da álgebra como disciplina pode ser visto como a organização de técnicas em torno da classificação e da resolução de equações, o que teve lugar no século IX, com os trabalhos de Al-Khwarizmi e de outros matemáticos ligados a ele.”
“Antes disso, é preciso citar os matemáticos indianos, em particular Bhaskara, para mostrar que ele não é o inventor da conhecida fórmula que ganhou seu nome no Brasil. Apesar de possuírem regras para resolver problemas que seriam hoje traduzidos por equações do 2º grau e usarem alguns símbolos para representar as quantidades desconhecidas e as operações, não se pode dizer que os indianos possuíssem uma fórmula de resolução de equações de 2º grau.”
“Os métodos para resolver problemas de 3º grau tiveram um papel importante na história da álgebra, passando por Omar Khayam, pelos matemáticos italianos e chegando a François Viète. Nesse caso, a origem da álgebra também pode ser associada à introdução do simbolismo. Há exemplos bastante expressivos de seu uso no Magreb (região do norte da África que abrange Marrocos, Saara Ocidental, Argélia e Tunísia) a partir do século XII. Na parte do Magreb próxima da Andaluzia, na Espanha, as práticas científicas são conhecidas por sua importância na transmissão da cultura antiga. A partir do século XIII, os tratados gregos começaram a ser traduzidos na Europa ocidental. No que tange ao uso de símbolos em problemas algébricos, citaremos exemplos das escolas de ábaco, que se desenvolveram na Itália entre os séculos XIII e XIV. Foi somente no século XV, porém, que parece ter havido um emprego mais sistemático da notação algébrica. A partir do tratamento das equações empreendido pelo italiano Girolamo Cardano, veremos que é possível definir, em um novo sentido, o que entendemos por álgebra.”
“Pretendemos mostrar que, se quiséssemos aplicar a alcunha de ‘o pai da álgebra’ a algum matemático do período, obteríamos múltiplas respostas: Diofanto, se usarmos a definição A para álgebra; Al-Khwarizmi, se usarmos a definição B; Cardano, se usarmos a C; e, finalmente, Viète, se usarmos a D. Ou seja, podemos concluir que alcunhas desse tipo são inúteis para a história da matemática.”
“Alexandria foi uma das cidades mais importantes da Antiguidade. Fundada em 331 a.C. por Alexandre, o Grande, permaneceu como capital do Egito durante mil anos, até a conquista muçulmana. Temos notícia de que o Museu de Alexandria, construído pelo rei Ptolomeu I por volta do ano 290 a.C., incluía uma grande biblioteca que reunia todo o saber da época. Inicialmente, seus pensadores mais conhecidos teriam sido Euclides e Arquimedes. Como, em seguida, a civilização grega se disseminou por uma vasta área, que ia do mar Mediterrâneo oriental até a Ásia Central, passou a incluir Alexandria. O período que chamamos de ‘helenístico’ se caracterizou pelo ideal de Alexandre de difundir a cultura grega aos territórios conquistados e se estendeu, de sua morte, em 323 a.C., até a anexação da Grécia por Roma, em 146 a.C.”
E se nunca houve o famoso incêndio da Biblioteca de Alexandria? E se nunca houve uma (tão suntuosa) Biblioteca de Alexandria? E se esse fosse um mito como o da Torre de Babel?
“Alexandria se tornou o centro da cultura grega na época helenística e seus habitantes eram, em sua maioria, gregos de todas as procedências, mas havia também uma colônia judaica e um bairro egípcio na cidade. Em seguida, passou a fazer parte do império romano, que se desenvolveu a partir da Itália e chegou a dominar terras da atual Inglaterra, França, Portugal, Espanha, Itália, partes da Alemanha, Bélgica, península Balcânica, Grécia, Turquia, Armênia, Mesopotâmia, Palestina, Egito, Síria, Etiópia e todo o norte da África. Muitas datas são comumente propostas para marcar o início do império romano, entre elas a da indicação de Júlio César como ditador perpétuo, em 44 a.C.”
“Hipátia, filha de Teon, astrônoma, matemática e filósofa do século IV, que se supõe ter sido assassinada durante um motim de cristãos no início do século V e cuja morte simboliza o fim da época de ouro da ciência alexandrina.” “Teon de Alexandria é, na verdade, o único dos matemáticos citados sobre o qual se pode assegurar que foi membro do Museu de Alexandria. O que se pode afirmar com certeza é que existe uma relação entre a conservação das obras científicas redigidas entre o século III a.C. e o século III d.C. e a conexão de seu autor à cidade de Alexandria. Ou seja, a influência da Biblioteca ou do Museu de Alexandria se exerceu sobre a conservação e a transmissão do conhecimento matemático, bem como sobre a seleção e a reprodução dos textos considerados relevantes.”
“Na astronomia, como nos indica o Almagesto, o sistema sexagesimal posicional passou a ser empregado para denotar a parte fracionária dos números. Além dessas evidências, existe, na matemática grega, uma série de questões que, por sua forma, lembram o modo como os cálculos babilônicos e egípcios eram enunciados. Como nos textos escolares mais antigos, o leitor é interpelado a realizar os passos ‘faça isso, coloque aquilo’. Tais prescrições, que aparecem nos escritos de Heron, invocam o que Vitrac (‘Dossier: les géomètres de la Grèce antique’) designa como ‘uma pedagogia pelo exemplo’. Apesar de evidências desse tipo, a ausência de fontes documentais não nos permite atestar com segurança a influência oriental sobre a matemática grega.”
“Um traço particular da escola de Alexandria é o enciclopedismo.¹ Os pensadores do período produziram numerosas enciclopédias, coleções, sínteses e todo tipo de iniciativas visando à organização do saber. Esses documentos não são especificamente matemáticos, estando ligados à orientação geral do governo da época, que incentivava a fundação de instituições para guardar e difundir o saber. O pensamento dos antigos merecia lugar de destaque, e devido à multiplicidade e ao acúmulo desse conhecimento era necessário organizar, selecionar, ou mesmo corrigir e completar, os autores estudados. O intelectual se configurava, assim, como um historiador do saber, pois precisava se situar em relação aos antigos, tratados com respeito e admiração.”
¹ Podemos, por conseguinte, chamar o movimento francês do XVII como neo-enciclopedismo, em contraposição.
“Antes da constituição da Coleção matemática, obra papiana célebre, seu livro VIII já havia circulado de forma autônoma com o título de Introduções mecânicas. Assim ele foi traduzido em árabe mais tarde, diferentemente dos outros livros da coleção.”
“nesse momento da Antiguidade tardia a matemática foi absorvida pelas escolas filosóficas, sobretudo as de inspiração neoplatônica. Essa tradição, na qual Proclus se encaixa, usava conceitos filosóficos para descrever, interpretar e criticar os trabalhos dos geômetras antigos. Os objetivos e métodos heurísticos dos antigos matemáticos podem ter sido então obscurecidos pela tendência formalista dos comentadores.”
“A história da matemática antiga escrita por Van der Waerden, muito influente nos anos 60-70, apresenta as Métricas, de Heron, como uma coleção de exemplos numéricos e sem provas, idêntica a um texto babilônico. Esse historiador chega a afirmar que, ao contrário das obras dos grandes matemáticos, o livro de Heron pode ser desconsiderado, uma vez que consiste somente de um texto aritmético de popularização. No entanto, todos os problemas das Métricas possuem uma demonstração. É verdade que muitas obras de Heron só foram descobertas no final do século XIX e início do XX, como é o caso, além desta, de seu comentário sobre os Elementos de Euclides. Esses textos, porém, não são compatíveis com a idéia de que Heron fosse um simples artesão.” Heron é o responsável por fazer a síntese epistemológica entre a geometria antiga e a ‘geodésia’ acima descrita.
“Para escaparmos da dicotomia entre teoria e prática, é preciso entender o que os antigos chamavam de ‘mecânica’, nomenclatura que pode designar 2 tipos de atividade. A primeira concerne à descrição, à construção e ao uso de máquinas, tendo um importante componente militar, particularmente impulsionado na época dos reis alexandrinos, quando a engenharia conheceu grandes progressos. Há, contudo, um outro tipo, que se interessa pelas causas que permitem explicar o funcionamento e a eventual eficácia das máquinas. Além dessas vertentes, nota-se também uma tentativa de redução da mecânica a princípios matemáticos oriundos da geometria. Por exemplo, métodos para resolver o problema da duplicação do cubo, e outros correlatos, eram vistos como mecânicos.” “Ambos [Heron e Pappus] defendiam a importância tanto filosófica quanto política da mecânica, em comentários que parecem se contrapor a outras opiniões desfavoráveis a ela.”
“Temos notícia, normalmente, de que no período romano o ensino da matemática era subordinado ao da filosofia ou das artes aplicadas, como a arquitetura, e consistia de ensinamentos simples, incluindo, no máximo, alguns resultados dos Elementos de Euclides ou do Almagesto de Ptolomeu. Entretanto, se era assim, como explicar que a Coleção matemática de Pappus, que claramente é direcionada para o grande público, contenha resultados de matemática tão avançada? No Capítulo 3, vimos como Pappus usava a intercalação na trissecção do ângulo, e esse é um pequeno exemplo, pois a Coleção matemática investiga diversos resultados sobre as cônicas de Apolônio, chegando a avançar teoremas originais.”
A VELHA FÁBULA DE MARX É AINDA MAIS VELHA: “As abelhas sabem intuitivamente o que lhes é útil, como o fato de que a área dos hexágonos, usados na fabricação das colméias, é maior do que a área dos quadrados dos triângulos. Contudo, só os matemáticos podem atingir conhecimentos mais elaborados.”
MECÂNICA ANTIGA, I.E., NADA MAIS DO QUE TRIGONOMETRIA TRIDIMENSIONAL IPSIS LITERIS: “A complementaridade entre geometria e mecânica pode ser exemplificada pelo uso de problemas equivalentes ao da duplicação do cubo na arquitetura, que enxergava sua utilidade prática ao permitir modificar um sólido de acordo com uma razão dada. Normalmente, o problema da duplicação do cubo devia ser resolvido por meio das seções cônicas, contudo, como é difícil desenhar cônicas no plano, outras soluções podiam ser obtidas com procedimentos mecânicos. Quando não era possível resolver problemas por meios geométricos, era lícito recorrer a instrumentos mecânicos.”
“Em geral, considera-se que a primeira ocorrência da notação simbólica que caracteriza nossa álgebra remonta ao livro Aritmética, escrito em grego por Diofanto. Acredita-se que esse autor tenha vivido no século III, ainda que tal data seja contestada. Além disso, embora se tenha notícia de que Diofanto viveu em Alexandria, não se pode assegurar que fosse grego, apesar de seu texto ser escrito nessa língua. O fato de sua obra parecer distinta da tradição grega levou até alguns historiadores, como Hankel, a conjecturar que ele fosse árabe. Não investigaremos os detalhes sobre sua origem. Interessa-nos aqui abordar a seguinte questão: pode-se concluir que o livro de Diofanto é o primeiro tratado de álgebra propriamente dito? Já houve muita discussão a esse respeito entre os historiadores, e forneceremos alguns argumentos contra e a favor dessa tese.
A contribuição mais conhecida de Diofanto é ter introduzido uma forma de representar o valor desconhecido em um problema, designando-o como arithmos, de onde vem o nome aritmética. O livro Aritmética contém uma coleção de problemas que integrava a tradição matemática da época. Já no livro I, ele introduz símbolos, aos quais chama ‘designações abreviadas’, para representar os diversos tipos de quantidade que aparecem nos problemas. O método de abreviação representava a palavra usada para designar essas quantidades por sua primeira ou última letra de acordo com o alfabeto grego:
ς (última letra da palavra arithmos, a quantidade desconhecida) (primeira potência)
ΔY (primeira letra de dynamis, o quadrado da quantidade desconhecida) (segunda potência)
KY (primeira letra de kybos, o cubo) (terceira potência)
ΔYΔ (o quadrado-quadrado) (quarta potência)
ΔKY (o quadrado-cubo) (quinta potência)
KYK (o cubo-cubo) (sexta potência)”
Método de Diofanto para nossa equação seguinte:
x + y = 20
xy = 96
Em que pese podermos fazer esse cálculo de cabeça espontaneamente (x = 12 e y = 8), em Diofant0, seguia-se o seguinte raciocínio:
Se x = y,
x = y = 10
xy = 100 (a segunda potência ou quadrado do número).
Logo,
100 – 96 = 4, que é a diferença para o produto realmente desejado.
Sendo 96 um produto, significa que este 4 é na verdade 2², ou seja, xy, se x = y, seria 4, e cada número desconhecido seria o 2.
Como inicialmente estipulou-se arbitrariamente que x = y = 10, soma-se e subtrai-se 2 deste número.
Portanto x = 12, y = 8.
Com os símbolos acima:
10 − ς + 10 + ς = 20
(10 − ς) (10 + ς) = 96
10² − ΔY = 10² − ς2 = 96
ς = 2
“Podemos perceber que o método não recorre a nenhuma construção geométrica para resolver o problema. Além disso, em sua resolução, opera-se com quantidades desconhecidas do mesmo modo como se lida com quantidades conhecidas. Para Diofanto, o arithmos é uma quantidade indeterminada de unidades diferente dos números, que são formados de uma certa quantidade, determinada, de unidades. No entanto, ambos são sujeitos ao mesmo tipo de tratamento. Por exemplo, assim como operamos com números, obtendo 1/3 ou ¼, podemos obter as partes dos arithmoi. A natureza das quantidades desconhecidas e as operações que podemos realizar com elas se baseiam nas propriedades dos números. Ou seja, na resolução de um problema as quantidades conhecidas e desconhecidas têm o mesmo estatuto. Somente por essa razão será possível introduzir um símbolo para uma quantidade desconhecida.
Na visão de alguns historiadores, o fato de se assumir uma representação para quantidades desconhecidas constitui um passo importante em direção à abstração. Logo, chegou-se a considerar Diofanto o ‘pai da álgebra’, uma vez que tal representação seria a principal característica de um pensamento algébrico. De modo mais cuidadoso, essa particularidade levou G.H.F. Nesselman (Die Algebra der Griechen) a designar o procedimento de Diofanto como uma ‘álgebra sincopada’ que faria a transição entre a álgebra retórica e a álgebra simbólica moderna. Mesmo Viète, segundo Nesselman, ainda praticava uma álgebra sincopada.”
“Heeffer, ‘On the nature and origin of algebraic symbolism’: esse autor mostra ser possível identificar, na história da álgebra, raciocínios simbólicos que não empregam símbolos. Ou seja, para fazer uma história sobre a emergência do simbolismo em matemática não basta procurar as fontes dos símbolos que usamos hoje, como fez Cajori em A History of Mathematical Notations.”
“Como vimos, no texto de Diofanto as quantidades desconhecidas são abreviadas, e não simbolizadas, o que já havia sido observado por J. Klein (Greek Mathematical Thought and the Origins of Algebra).”
“J. Christianidis (‘The way of Diophantus: Some clarifications on Diophantus’ method of solution’) também se distancia da interpretação algebrizante sobre Diofanto ao mostrar que uma parte essencial de seu método consiste na tradução dos termos numéricos, que constam no enunciado do problema, em designações abreviadas, que podem ser vistas como termos técnicos pertencentes a uma teoria aritmética. Presume-se que essa teoria já existisse antes de Diofanto e possuísse uma linguagem própria, distinta da que é adotada no enunciado do problema.”
“Fica claro que a técnica continuaria a funcionar, caso esses números fossem substituídos por outros, mas isso não chega a ser feito. Diofanto fornece uma enorme variedade de soluções que funcionam para exemplos particulares, enumerados à exaustão. Porém, não existem métodos de solução como os nossos, descritos, de modo geral, com o auxílio de símbolos para representar os coeficientes e podendo ser aplicados aos exemplos.”
“A maior parte da matemática que conhecemos como ‘indiana’ foi escrita em sânscrito e se originou na região do sul da Ásia (que compreende também o Paquistão, o Nepal, Bangladesh e Sri Lanka). Os registros mais antigos de que temos notícia datam da primeira metade do primeiro milênio antes de Cristo, mas se tornaram mais freqüentes depois da conquista de Alexandre, o Grande, no século IV a.C. Não conhecemos bem as interações da matemática indiana com as tradições antigas, entretanto, alguns de seus problemas parecem ter sido inspirados pelo contato com a astronomia babilônica e grega.
É sabido que o sistema de numeração decimal posicional que usamos hoje é de origem indiana, tendo sido transmitido para o Ocidente pelos povos islâmicos na Idade Média. E os documentos indianos mostram que esse sistema estava bem-estabelecido nos primeiros séculos de nossa era. Antes disso, usavam-se diferentes sistemas de numeração, aditivos e multiplicativos, embora não posicionais. Alguns textos astronômicos e astrológicos do século III já empregavam um sistema posicional decimal, incluindo um símbolo para o zero. No entanto, as evidências sobre a astronomia escrita em sânscrito só se tornaram mais significativas a partir de meados do primeiro milênio. Elas mostram que havia, nesse período, uma intensa atividade matemática expressa sobretudo pela elaboração de tratados astronômicos que também foram influenciados por obras gregas, devido ao contato com o império romano. Os autores integravam elementos de sua tradição matemática – como conceitos sobre a astronomia e o calendário, bem como o sistema posicional decimal – a outros componentes, adaptados das obras gregas – como a trigonometria plana, os modelos cosmológicos geocêntricos (como os de Ptolomeu) e a astrologia.
Dos tratados desse tipo o mais antigo que conhecemos foi escrito por Aryabhata, que nasceu no ano 476. Pouco se sabe sobre sua vida, mas essa obra permanece uma das fontes mais importantes sobre a matemática e a astronomia indianas. Ela foi toda escrita em versos, o que se tornou uma tradição indiana, e apresenta conhecimentos matemáticos variados, principalmente em relação às regras de cálculo. Há procedimentos aritméticos e geométricos, como os usados para encontrar raízes quadradas e cúbicas, assim como o cômputo de áreas, além de incluir regras trigonométricas úteis para a astronomia. O aspecto mais inovador é a sistematização das técnicas de cálculo, que constituem uma prática chamada ‘ganita’, concebida como o estudo dos métodos de cálculo em geral e voltados não somente para a astronomia.
Como a exposição em versos era de difícil compreensão, as obras indianas eram complementadas por comentários redigidos por outros matemáticos tendo em vista elucidar o seu significado. O comentário mais antigo sobre o livro de Aryabhata foi escrito por um autor de nome Bhaskara em 629. Mas esse personagem é completamente desconhecido e chamado, freqüentemente, de Bhaskara I, para distingui-lo do outro Bhaskara mais famoso, que viveu no século XII. O comentário de Bhaskara I indica que a matemática documentada em sânscrito era bastante rica, pois ele se refere a uma tradição que parecia estar bem-estabelecida. Essa tradição diz respeito a uma prática distinta da que concebemos hoje como matemática, pois seu principal objetivo era garantir que os leitores compreendessem e interpretassem corretamente as regras contidas nos versos, que pareciam propositadamente criptográficos. Sua decodificação incluía, ainda, uma análise gramatical, considerada parte da prática matemática.
Um tratado astronômico contemporâneo do comentário de Bhaskara I foi escrito pelo astrônomo Brahmagupta, em 628. Um dos capítulos matemáticos de seu tratado é dedicado completamente à ganita, contendo o estudo de operações aritméticas, razões e proporções, juros, bem como fórmulas para achar comprimentos, áreas e volumes de figuras geométricas. Contudo, havia também um capítulo dedicado a um outro tipo de matemática que compreendia análises envolvendo o zero, os negativos e positivos, as quantidades desconhecidas, e ainda os métodos de eliminação do termo médio e de redução a uma variável. Tratava-se de técnicas para lidar com problemas envolvendo quantidades desconhecidas.”
“Os procedimentos utilizados por Brahmagupta foram citados, mais tarde, por Bhaskara II, autor dos livros mais populares de aritmética e álgebra no século XII, que, presume-se, foram livros-textos voltados para o ensino. As evidências abundantes sobre os trabalhos desse astrônomo, que nasceu em 1114, indicam que eram bastante influentes na época. Seus livros mais conhecidos, o Lilavati e o Bija Ganita (Semente do Cálculo), mostram como a prática da ganita, já presente nos escritos de Aryabhata e Brahmagupta, amadureceu ao longo dos séculos.”
“(II) Seja uma igualdade contendo a quantidade desconhecida, seu quadrado, etc. Se temos os quadrados da quantidade desconhecida etc., em um dos membros multiplicamos os dois membros por um fator conveniente e somamos o que é necessário para que o membro das quantidades desconhecidas tenha uma raiz; igualando, em seguida, essa raiz à do membro das quantidades conhecidas, obtemos o valor da quantidade desconhecida.
Observamos que se concebia, de modo retórico, uma igualdade entre dois membros, sem utilização do sinal de igual: a igualdade entre um membro contendo a quantidade desconhecida (e o seu quadrado) e outro membro contendo as quantidades conhecidas. O primeiro membro deve ser escrito de modo a possuir uma raiz, ou seja, deve ser reescrito como um quadrado”
“De um enxame de abelhas, tome a metade, depois a raiz. Esse grupo extrai o pólen de um campo de jasmins. Oito nonos do todo flutuam pelo céu. Uma abelha solitária escuta seu macho zumbir sobre uma flor de lótus. Atraído pela fragrância, ele tinha se deixado aprisionar na noite anterior. Quantas abelhas havia no enxame?” O modo indiano de dizer x + 16x²/9 + 2 = 2x²! “o número de abelhas, 2x² = 72.”
“Na matemática indiana eram muito comuns as equações com mais de uma incógnita, equações indeterminadas que escreveríamos, hoje, assim: xy = ax + by + c ou y2 = ax² + 1. Esses casos eram resolvidos por procedimentos semelhantes ao método descrito acima, podendo se empregar símbolos para representar as incógnitas. O método de Bhaskara funciona perfeitamente para resolver o que chamamos, hoje, de ‘equações de 2º grau’, mas ainda assim não podemos atribuir-lhe a invenção da fórmula usada atualmente. Por quê? Mesmo que pudessem ser empregados símbolos para representar as incógnitas e algumas operações, não havia símbolos para expressar coeficientes genéricos a, b e c,… de uma equação (…) o que será proposto por Viète somente no século XVI.
A predominância dos textos de Bhaskara II faz com que pensemos que a matemática indiana decaiu depois do século XII, mas há evidências de que ela continuou a se desenvolver, embora de forma isolada em relação à Europa. Transmissões diretas da matemática indiana para o Ocidente foram freqüentes durante a expansão islâmica, que controlou parte da Índia a partir do século VIII. Os tratados astronômicos da escola de Brahmagupta chegaram a Bagdá nessa época e foram rapidamente traduzidos. Outras traduções do sânscrito inspiraram trabalhos árabes em astronomia e astrologia, alguns imitando a escrita em versos. A maioria desses textos se perdeu. Contudo, ainda assim podemos afirmar que a astronomia emergente na matemática árabe adotou diversos métodos indianos, embora de modo não-uniforme, como a representação decimal posicional e as técnicas de cálculo. No entanto, a influência indiana do período inicial logo foi ultrapassada pela invasão de textos matemáticos e astronômicos gregos, traduzidos em seguida. A astronomia indiana foi, então, submetida às práticas greco-islâmicas, tendo permanecido somente uma aritmética decimal posicional, designada de ‘computação indiana’.”
“alguns problemas recreativos, propondo desafios, parecem ter atravessado os séculos. Seria o caso, por exemplo, do jogo do tabuleiro de xadrez, que consiste em perguntar quantos grãos de arroz obteremos se colocarmos um grão na primeira casa do tabuleiro e duplicarmos sucessivamente o número de grãos até chegar à última casa.”
“Houve uma primeira fase bastante tolerante do Islã, em que se permitia a convivência dos muçulmanos com os judeus e os cristãos. Do ponto de vista do pensamento, essa tolerância também era sentida, pois, ao lado das ciências sagradas, constituídas pela teologia e pela jurisprudência, estavam as chamadas ciências estrangeiras, recebidas dos gregos. Estas eram constituídas por ramos do conhecimento tidos como auxiliares que podiam servir à ciência tradicional, incluindo a matemática e a astronomia.” Bom, sem Química não ‘se fazem’ homens-bomba…
“Alguns problemas práticos exigiam o desenvolvimento da matemática, caso das heranças. Toda a família tinha direito a uma parte da herança, mas não de modo igualitário. Eram usados métodos aritméticos sofisticados que passavam por cálculos com frações, e ainda o método da falsa-posição, para encontrar uma quantidade desconhecida. Teriam surgido daí os primeiros problemas, enunciados de modo retórico, que são equivalentes ao que designamos hoje por meio de uma equação do 2º grau.”
O MITO UBÍQUO DA “GRANDE BIBLIOTECA”: “Um outro fator de desenvolvimento da matemática árabe, mais conhecido, são as traduções das obras gregas, que começaram a ser feitas por volta do século VIII. Essas iniciativas são atribuídas a indivíduos ou grupos de estudiosos que se interessavam voluntariamente pelos escritos encontrados nos territórios conquistados. As instituições de ensino eram as madraças, dedicadas à difusão do conhecimento, mas não à sua produção. Tais escolas eram mantidas por fundações piedosas e deviam ensinar os textos canônicos, mantendo a tradição do saber sagrado. No entanto, nesse primeiro momento, várias delas apoiavam também as ciências estrangeiras. No período racionalista, entre os séculos IX e XI, houve ainda uma instituição oficial importante, fundada pelo califa em Bagdá e conhecida como Casa do Saber. Aí existia uma biblioteca na qual se colecionavam e traduziam manuscritos gregos. Além desta, havia algumas outras bibliotecas e observatórios em que também era possível estudar as ciências estrangeiras.”
“Ahmed Djebbar (Une histoire de la science arabe) mostra que o fenômeno de tradução não foi instantâneo, nem seguiu uma ordem racional. Não havia nenhuma política central relativa ao saber e ninguém decidiu impetrar um programa de tradução das obras científicas antigas e confiá-las a uma equipe de tradutores. As traduções seguiram uma dinâmica complexa e descoordenada. Os primeiros tradutores encontravam obras antigas e propunham um texto em árabe contendo vários erros, pois não existiam correspondentes em árabe para os termos científicos que constavam dessas obras. Muitos eram os casos, portanto, de retraduções ou mesmo de reconstruções dos textos antigos, o que pode ter propiciado a emergência das primeiras contribuições originais dos pensadores árabes.”
ARISTÓTELES SEMPRE DESTRUINDO O LEGADO PLATÔNICO, EM VÁRIAS ERAS E POVOS: “Em um primeiro momento, as obras de medicina e filosofia despertaram um grande interesse, mas os árabes traduziam praticamente tudo o que encontravam, sem critério de seleção rígido. Aos poucos, os trabalhos de Aristóteles se destacaram e sua obra dominou as discussões filosóficas entre os séculos IX e XIII. Essa influência, no entanto, não foi necessariamente positiva para a matemática árabe, pois impunha limites, por exemplo: o ‘um’ não devia ser considerado número; o movimento devia ser banido das demonstrações geométricas; devia ser respeitada a homogeneidade das grandezas. Ou seja, a influência filosófica impunha um padrão geométrico à álgebra, ainda que essa restrição não fosse significativa.”
“Entre os séculos VIII e XII, a cidade de Bagdá era um dos maiores centros científicos do mundo, e seus matemáticos tinham conhecimento tanto das obras gregas quanto das orientais. A partir do século IX, essa cultura evoluiu para uma produção matemática original que tinha na álgebra um de seus pontos fortes. A grande influência das obras clássicas não impediu o surgimento de uma matemática nova, e o matemático mais ilustre desse século foi Al-Khwarizmi. No século XI houve uma dogmatização do Islã e os racionalistas foram vencidos. (…) A reconquista de Toledo, Córdoba e Sevilha, no século XII, fez com que os núcleos científicos dessas cidades andaluzas migrassem para um espaço muçulmano mais acolhedor para a sua cultura. Tal mudança impulsionou o desenvolvimento da matemática e da astronomia no Magreb entre os séculos XII e XIV.” Navegar ainda não era, mas seria preciso. E para navegar, carecia calcular…
“Entre os séculos XII e XV, Marrakech era um polo de desenvolvimento científico, unificando as culturas africanas e européias localizadas em torno do Mediterrâneo, sem distinção entre muçulmanos, judeus e cristãos. Além de enfatizar contribuições matemáticas antes desconhecidas, como a introdução do simbolismo algébrico, essas pesquisas recentes analisam o papel dessas regiões no fenômeno de circulação da produção matemática em direção ao restante da Europa, por meio de traduções para o latim e o hebraico. Essa direção de pesquisa busca desconstruir o viés eurocentrista do relato tradicional, explícito nos escritos dos primeiros historiadores da matemática, que eram matemáticos de profissão e viam com preconceito a contribuição árabe”
“Para o quarto caso, Al-Khwarizmi considera o exemplo ‘um Mal e dez Jidhr igualam 39 dinares’, que em nossa notação algébrica seria representado como x² + 10x = 39. O algoritmo de resolução era descrito assim:
Tome a metade da quantidade de Jidhr (que neste exemplo é 5)
Multiplique essa quantidade por si mesma (obtendo 25)
Some no resultado os Adad (fazemos 39 + 25 = 64)
Extraia a raiz quadrada do resultado (que dá 8)
Subtraia desse resultado a metade dos Jidhr, encontrando a solução (essa solução é 8 − 5 = 3)”
“Observando a terceira coluna da tabela, percebemos que o algoritmo de resolução é uma sequência de operações equivalentes à fórmula de resolução de equação do 2º grau usada atualmente. Mesmo que fosse exposto para um exemplo particular, o método descrito por Al-Khwarizmi permitia tratar qualquer exemplo dentro de um caso determinado, logo, esse método gozava de certa generalidade.”
“Observemos que esse modo de ‘passar para o outro lado’ não se justifica pela concepção que temos de que a soma e a subtração são operações inversas. O modo de operar dos árabes está mais próximo da crença de que realmente retiramos uma quantidade de um lado para ‘passar para o outro lado’, forçada pela restrição ao universo dos números positivos. Em seguida, as espécies do mesmo tipo e iguais são subtraídas de ambos os lados, o que seria equivalente a retirar 58 de ambos os lados. É preciso equilibrar os dois lados, ou seja, balanceá-los pelo procedimento de al-muqabala, reduzindo os dois números a um só.”
“Nessas práticas subcientíficas pode ser sentida uma influência indiana indireta. Um dos principais exemplos é o uso dos algarismos que designamos como ‘indo-arábicos’. Essa representação dos números, presente também em nossa matemática, já era empregada por Al-Kwharizmi e é atribuída por ele aos indianos. No entanto, esta deve ter sido uma herança de praticantes que usavam o sistema, não sendo transmitida por tratados aritméticos de natureza científica. Ainda assim, é discutível se o sistema posicional decimal, adotado pelos indianos, foi divulgado pelos árabes, pois estes usavam majoritariamente o sistema grego sexagesimal.”
“As práticas algébricas dos árabes possuem conexão com os métodos babilônicos e indianos, porém é difícil encontrar evidências que testemunhem influências diretas dessas culturas. Antes mesmo dos tempos islâmicos, tais tradições já haviam se misturado e, a partir do século IX, a síntese islâmica foi responsável pela sistematização das práticas.”
“Além disso, alguns indianos operavam com quantidades negativas, o que os árabes, nessa época, não faziam. Nem Bhaskara, nem outro matemático indiano, nem Al-Khwarizmi, nem outro árabe qualquer inventou a fórmula para a resolução da equação de 2º grau, apesar de todos eles saberem resolver o análogo a uma equação desse tipo nos termos da matemática de seu tempo. É certo que a fórmula só pôde ser escrita depois que Viète introduziu um simbolismo para os coeficientes, como veremos adiante, mas nem mesmo ele pode ser considerado o inventor da fórmula, uma vez que seu método de resolução já era amplamente conhecido pelos indianos e árabes.”
“No caso de situações envolvendo quantidades elevadas ao cubo, Al-Khayam reconhece não ter sido possível encontrar um algoritmo análogo ao que tinha sido utilizado para equações quadráticas, por esse motivo suas soluções são geométricas e empregam cônicas.”
“Por exemplo, o problema 21 (‘um cubo, algumas raízes e um número são iguais a alguns quadrados’), traduzido em linguagem atual, corresponde à equação x³ + bx + a = cx².”
“Pela lei de homogeneidade das grandezas, todos os seus termos são considerados volumes, ou seja, de grau 3. Isso quer dizer que um cubo deve ser somado a cubos ou paralelepípedos. Logo, a expressão ‘algumas raízes’ do enunciado (traduzida como bx) era usada para designar um paralelepípedo cuja altura é a raiz e cuja base é obtida tomando-se um certo número de vezes um quadrado unitário.”
“O método empregado por Al-Khayam era puramente geométrico, diferente do caso da equação do 2º grau, que envolve a extração de uma raiz quadrada, por isso ficou conhecido como ‘método de resolução por radicais’. Será devido à busca de um método de resolução por radicais para as equações cúbicas que grande parte da álgebra se desenvolverá nos séculos XV e XVI.”
“Fibonacci incontestavelmente, tem o papel de pioneiro no renascimento da matemática no oeste cristão. Como nenhum outro antes dele, considerou de modo novo o conhecimento antigo e desenvolveu-o de maneira independente. Em aritmética, mostrou habilidade superior para os cálculos. Além disso, ofereceu aos seus leitores um material organizado de forma sistemática e ordenou seus exemplos do mais fácil para o mais difícil (…) Em geometria demonstrou, diferentemente dos agrimensores, um domínio completo de Euclides, cujo rigor matemático ele foi capaz de recapturar.” Gillispie, Dictionary of Scientific Biography
“Esse relato é comum em livros de história da matemática. Uma radicalização dessa lenda sobre o ‘renascimento’ da matemática antiga na Europa aponta que, com a queda de Constantinopla, em 1453, refugiados que escaparam para a Itália teriam levado preciosos tratados gregos antigos para o mundo europeu ocidental. A verdade é que alguns tratados gregos já haviam aparecido na Europa no século XIII, quando as cruzadas, ao invés de se dirigirem à Terra Santa, invadiram outro território cristão, Constantinopla, onde havia manuscritos conservados desde a Antiguidade, quando a região ainda era grega e se chamava Bizâncio.
É fato que Fibonacci freqüentou Bugia, cidade da Argélia, seguindo o desejo de seu pai, que era comerciante. Depois dessa primeira formação em matemática, Fibonacci viajou pelo Egito, pela Síria, pelo sul da França e pela Sicília, na Itália. Ou seja, teve contato com o mundo mediterrâneo, onde se aperfeiçoou em domínios como a álgebra, prática até então desconhecida dos europeus. No entanto, a versão simplificadora sobre a difusão da álgebra na Itália teve de ser reformulada nos últimos anos devido a dois complicadores: as descobertas que exibem o desenvolvimento de uma álgebra simbólica no Magreb e na Andaluzia entre os séculos XI e XIV, bem como sua transmissão para os cristãos na Espanha; e as pesquisas em torno das escolas de ábaco, que floresceram na Itália a partir do século XIII.
Essas escolas, que treinavam jovens comerciantes desde os 11 ou 12 anos em matemática prática, e se difundiram em várias regiões da Itália, sobretudo Florença, estão relacionadas ao desenvolvimento do capitalismo no fim da Idade Média. Para tratar problemas ligados ao comércio, ensinava-se o cálculo com numerais indianos (…), a regra de três, os juros simples e compostos, os métodos da falsa-posição, entre outras ferramentas voltadas para problemas práticos. Ainda que fossem designadas como escolas de ábaco, a partir do século XIII elas se dedicavam a técnicas de cálculo sem ábaco.”
“O livro mais conhecido de Fibonacci se chama Liber Abaci, ou seja, ‘livro de ábaco’, o que levou alguns historiadores a afirmarem que, em geral, os escritos associados às escolas de ábaco eram, de fato, resumos e adaptações dessa obra de Fibonacci. Esses textos de matemática prática, escritos em língua vernácula, receberam pouca atenção dos historiadores até as transcrições feitas por Gino Arrighi e seus colegas italianos, nos anos 1960 e 70.”
“Na Europa do século XVI, desenvolveram-se pesquisas dedicadas à resolução de equações que empregavam uma grande quantidade de símbolos e que estão na origem de alguns dos que conhecemos até hoje. Os símbolos de + (mais) e − (menos) já eram usados na Alemanha. O símbolo para raiz quadrada, por exemplo, foi introduzido em 1525 pelo matemático alemão Christoff Rudolff. Seu aspecto vem de uma abreviação da letra r, inicial de ‘raiz’. Em 1557, o inglês Robert Recorde publicou um livro de álgebra no qual introduziu o símbolo ‘=’, usado por nós para a igualdade: um par de retas paralelas, pois ‘não pode haver duas coisas mais iguais’. Os símbolos para o quadrado e o cubo da quantidade desconhecida provinham de abreviações das palavras latinas.”
“A padronização dos símbolos matemáticos se deu muito mais tarde, a partir do final do século XVII, sobretudo devido à popularidade dos trabalhos de Descartes, Leibniz e Newton, conforme será visto nos capítulos seguintes.”
“Quantidades negativas já tinham aparecido em problemas mais simples, envolvendo equações do 2º grau. Nesse caso, no entanto, quando a quantidade negativa aparecia no resultado, era fácil driblar a dificuldade – bastava dizer que a equação não tinha solução. A aplicação da fórmula para resolver equações do 3º grau faz com que não seja possível desviar da questão com facilidade. As equações irredutíveis serão tratadas por Rafael Bombelli, matemático italiano do século XVI associado à história dos números complexos.”
“François Viète, que viveu entre os anos 1540 e 1603, introduziu uma representação padrão: as incógnitas serão representadas pelas vogais e os coeficientes pelas consoantes do alfabeto, todas maiúsculas”
“É importante observar que há uma diferença de natureza fundamental entre uma ‘incógnita’ e um ‘coeficiente’. A incógnita é uma quantidade desconhecida que será conhecida a partir das restrições representadas pela equação; já o coeficiente é uma quantidade conhecida genérica que está, portanto, indeterminada na expressão de uma equação qualquer. Ambos os casos pressupõem indeterminações, porém em níveis distintos: a determinação dos coeficientes é obtida pela escolha de uma equação particular (arbitrária); e a determinação do valor da incógnita, pela resolução (não-arbitrária) dessa equação. A determinação da incógnita depende das restrições dadas por uma equação. De modo distinto, no universo das equações, a escolha arbitrária de coeficientes determina uma equação. Por exemplo, na equação ax² + bx + c = 0 a escolha dos valores a = 1, b = 3 e c = 100 determina um ‘caso’: x² + 3x + 100 = 0. A notação introduzida por Viète deveria ter representado, portanto, uma generalização dos métodos algébricos.”
“A REVOLUÇÃO CIENTÍFICA É COMPREENDIDA, comumente, como uma brusca mudança no modo de fazer ciência ocorrida nos séculos XVI e XVII, em especial na astronomia, na física e na matemática. Copérnico teria inaugurado o questionamento da cosmologia aristotélica e ptolomaica; novas teorias teriam sido formuladas a partir das leis de Kepler; e Galileu seria o responsável pelo desenvolvimento de uma nova física, baseada em uma visão mecânica da natureza que pode ser descrita em linguagem matemática. Esse processo culminaria com Newton, que teria reunido tais avanços de modo coerente e representaria o triunfo da ciência moderna.
O século XVII é visto como a ‘alvorada da matemática moderna’, título do capítulo que H. Eves dedica ao período em sua Introdução à história da matemática. Na historiografia tradicional, o papel de Descartes e de suas contribuições à geometria aparece ora desconectado desse contexto mais amplo, ora como uma conseqüência vaga, no máximo de natureza filosófica. No primeiro caso, esquece-se que sua Geometria foi publicada como anexo de um livro filosófico que também incluía um texto de ótica, além do fato de ele ter abordado diferentes problemas de física.” “o matemático francês é considerado moderno e suas principais contribuições, como o plano cartesiano, são explicadas por meio da notação atual. Essa abordagem leva a um dos inconvenientes mais graves na história da matemática a partir desse período: a subdivisão desse saber em disciplinas. Descartes e Fermat são mencionados como fazendo parte da história da ‘geometria analítica’, como se essa designação fizesse sentido antes deles. No entanto, como falar da história de certo domínio matemático se queremos analisar, de modo amplo, os procedimentos que só mais tarde foram selecionados e traduzidos com a finalidade de integrar esse domínio?”
CAPÍTULO 5. A Revolução Científica e a nova geometria do século XVII
“Numerosos exemplos mostram que a história da ciência nessa época não é tão triunfal como se acredita, e que a historiografia tradicional construiu esse cânone para justificar a imagem moderna da ciência. Na verdade, a recepção das idéias inovadoras de Copérnico, Galileu e Newton parece ter sido bastante lenta; a convivência entre as novas e as antigas idéias gerou misturas no pensamento; e eles não escreveram com o intuito nítido de renovar os padrões que os precediam.”
“Alguns estudos que exibem a complexidade de interesses dos pensadores da época podem ser encontrados em M. Osler (org.), Rethinking the Scientific Revolution.”
“A matemática era estudada para ajudar na compreensão das proposições aristotélicas sobre a lógica e a natureza; a aritmética consistia em regras de cálculo; a geometria era tirada de Euclides e de outras geometrias práticas; a música era influenciada por Boethius; e a astronomia seguia a tradição de Ptolomeu e das traduções de trabalhos árabes.”
“A escola típica do período anterior era monástica e rural; agora inauguravam-se escolas urbanas de vários tipos, com objetivos amplos. Ainda que o programa pudesse variar de uma escola para outra, segundo o interesse do professor que a dirigia, as escolas, de modo geral, reorientaram o currículo para satisfazer às necessidades práticas de uma clientela variada que ocuparia postos de direção na Igreja e no Estado. Com isso, o currículo passou a incluir, além da teologia, a lógica, o quadrivium matemático, a medicina e o direito”
“Estrangeiros que não sabiam árabe chegavam à Espanha, procuravam um professor e começavam a traduzir; ou encontravam um nativo bilíngüe e faziam versões em parceria. Um exemplo desse segundo tipo foi Robert de Chester, de Gales, que propôs a primeira tradução da Álgebra de Al-Khwarizmi, em 1145.”
“Até o século XIII, o ensino era de responsabilidade de mestres que se estabeleciam com o apoio de uma escola ou de modo autônomo. Com o crescimento dessas iniciativas, foi necessário organizá-las. Os mestres e estudantes começaram então a formar associações chamadas ‘universidades’ (…) Essa nomenclatura, no entanto, só era usada em Bolonha, onde os alunos se organizavam e contratavam os professores. As universidades não se caracterizavam por edifícios ou estatutos; eram grupos de professores que podiam ter mobilidade. Um dos principais objetivos dessas corporações era o autogoverno e o monopólio, ou seja, o controle do ensino. Assim, elas acabaram obtendo o direito de estabelecer os próprios padrões, como fixar o currículo, conceder diplomas e determinar quem podia estudar e ensinar. Tudo isso com o apoio do mecenato de papas, imperadores ou reis.”
“A astronomia ainda era respeitada, ao passo que a aritmética e a geometria mereciam um ensino breve e superficial. Tais matérias eram destinadas à formação de jovens dentro da faculdade de artes e tinham uma função propedêutica para a entrada nas faculdades superiores, onde o saber englobava somente a teologia, a jurisprudência e a medicina.”
“para Aristóteles, os elementos do cosmos sempre se comportaram e se comportarão de acordo com sua natureza. Logo, para ele, não houve um momento em que o Universo nasceu, nem haverá um outro em que deixará de existir. Ora, do ponto de vista cristão, tal posição é indefensável”
“Em Paris, entre 1210 e 1277, houve diversas condenações às teses de Aristóteles, sobretudo à sua física. No entanto, a atenção às causas naturais dos fenômenos já havia atraído diversos pensadores, e a filosofia natural continuou a se desenvolver no século XIV, ainda que prolongando as tentativas de conciliação com as doutrinas cristãs. Esse século foi marcado pela influência de São Tomás de Aquino, que reconciliou o aristotelismo e a Igreja.”
“Oresme utilizava esse diagrama para demonstrar uma lei que já havia sido formulada pelos cientistas de Oxford e que versava sobre a quantidade total de uma qualidade. Afirmava-se que: dada uma qualidade uniformemente disforme em um intervalo de tempo, a sua quantidade total é igual à quantidade total da qualidade uniforme que afeta o corpo com a intensidade média da qualidade uniformemente disforme.” [!]
O homem vitruviano de Da Vinci.
“Peuerbach lecionava em Viena, conhecia perfeitamente o Almagesto e aperfeiçoou as tábuas astronômicas de Ptolomeu usando os instrumentos que inventava. Quando foi convidado para ir à Itália, levou Regiomontanus, que viria a completar seu trabalho depois de sua morte, em 1461. A obra de Peuerbach é uma iniciativa característica do século XV, pois tentava conciliar os ideais aristotélicos com a astronomia de Ptolomeu. Seu livro principal, Theoricae novae planetarum (Novas teóricas dos planetas), publicado por Regiomontanus, exerceu grande influência sobre Copérnico.”

O “último” modelo geocêntrico (antes da emergência da neo-imbecilidade, vulgo Terraplanismo).
“Sua obra De revolutionibus orbium coelestium (Da revolução das esferas celestes) foi publicada no ano de sua morte, em 1543, embora sua teoria já fosse conhecida. Algumas tabelas astronômicas baseadas em suas obras começaram a ser usadas por volta de 1550, e a atração que o trabalho de Copérnico exercia se devia, principalmente, ao fato de oferecer um meio mais simples e mais acurado para calcular a posição dos astros. Ou seja, sua importância, para a época, não era atribuída ao fato de ter fornecido um modelo físico mais exato dos movimentos celestes. O traço inovador da teoria de Copérnico então reconhecido era a defesa da autonomia dos modelos matemáticos para salvar as aparências dos fenômenos.”
“A explicação física no estilo ptolomaico/aristotélico, exemplificada pela obra de Peuerbach, permaneceu sendo a principal referência para a astronomia até os anos 1570, quando as observações realizadas por Tycho Brahe abriram novas possibilidades. Somente por volta de 1600 os astrônomos europeus pareciam estar preparados para aceitar a realidade física do sistema heliocêntrico.”
“Normalmente, o Renascimento é identificado com o espírito platônico, pelo privilégio ocupado pela matemática como ferramenta explicativa. Mas a influência de Platão não parece ter sido especialmente forte se comparada à de outros pensadores gregos, como Arquimedes. A Europa ocidental conheceu os tratados mecânicos de Arquimedes com as traduções do século XIII, entretanto, só começou realmente a se apropriar de seus trabalhos no século XVI. Esse renascimento da mecânica clássica não se deveu à atuação das universidades nem dos humanistas e sim de engenheiros interessados em questões teóricas, como Niccolò Fontana, conhecido como Tartaglia.” “Tartaglia publicou sua Nova scientia em um dialeto local em 1537. A nova ciência mencionada nessa obra é a balística, que traduz as preocupações com o estudo da artilharia em longas distâncias e demanda a análise da trajetória de projéteis.”
“A Coleção matemática de Pappus foi traduzida em 1588 e fez ressurgir o interesse pelas construções dos gregos, chamadas de problemas de lugares geométricos (locus). Pappus os classificava como: problemas planos, construídos com régua e compasso; problemas sólidos, construídos por cônicas; e problemas lineares, construídos por curvas mais gerais, como a espiral. Além da obra de Pappus e dos trabalhos algébricos então disponíveis, em 1575 foi publicada uma tradução para o latim da Aritmética de Diofanto. A Arte analítica de Viète foi influenciada por esses trabalhos. No entanto, para resolver problemas geométricos, ele propunha usar uma argumentação denominada ‘análise’. A obra publicada por Viète em 1591, que em latim se intitula In Artem Analyticem Isagoge (Introdução à arte analítica), é o primeiro dos 10 tratados que formam a sua Opus restituta Mathematica Analyseos, seu, Algebra nova (Obra de análise matemática restaurada, ou Álgebra nova). Nesse título a palavra que chama a atenção é restitua, levando-nos a acreditar que Viète queria ‘restaurar’ a análise dos antigos. Dando seqüência à Isagoge, ele apresentou o Les Zeteticorum libri quinque (Cinco livros das zetéticas), nos quais aplica sua arte analítica a 82 problemas que são, em sua maioria, análogos aos estudados por Diofanto na Aritmética. A Arte analítica começa com uma explicação do que é análise, retirada da Coleção matemática de Pappus”
“pelo método analítico, supomos que as soluções desconhecidas são conhecidas e operamos com elas como se fossem conhecidas, até chegar a um resultado conhecido que determina a solução. A simbolização algébrica permite representar essas soluções desconhecidas por símbolos, manipulados segundo as mesmas regras que os números conhecidos.” “Quando escrevemos x + 2 = 3, tratamos o x como se fosse conhecido e operamos com essa quantidade da mesma forma que fazemos com o 3 e o 2, que são, efetivamente, números conhecidos. Com essa manipulação, fazemos x = 3 − 2 = 1 e encontramos o valor da quantidade desconhecida. Operamos, nesse exemplo, com as quantidades procuradas como se elas já estivessem dadas. Se quiséssemos resolver o problema de encontrar duas grandezas com soma e produto dados pelo método analítico, começaríamos supondo que essas grandezas que procuramos são dadas e podem ser chamadas de x e y.”
“Alguns matemáticos do século XVI, como Viète, e mesmo Descartes, no século XVII, acreditavam que os gregos omitiam, na maioria das vezes, a parte referente à análise das resoluções dos problemas. Para os antigos, a análise seria então um método de descoberta, e não de demonstração.”
“NULLUM NON PROBLEMA SOLVERE (‘nenhum problema sem resolver’). Foi para alcançar esse objetivo que inventou o que chamou de logistica speciosa, que se propunha a ser uma ciência dentro dos padrões gregos. Tratava-se, na verdade, de uma nova maneira de calcular, apresentada na forma axiomática.” “Um único símbolo deveria poder representar todos os tipos de grandeza. Ao fundar um cálculo para todos os tipos de grandeza (numérica ou geométrica; conhecida ou desconhecida), Viète poderia resolver todos os problemas.”
“O lugar de Galileu na transformação da ciência no século XVII foi objeto de intensas controvérsias. Uma das polêmicas mais famosas envolve as teses do historiador e filósofo da ciência Alexandre Koyré. Segundo Koyré, as práticas empíricas em áreas como balística, fortificação e hidráulica ajudaram a derrubar o feudalismo e o poder medieval, mas não poderiam ser suficientes para transformar a ciência do movimento. Em diversos artigos, escritos em torno dos anos 40, Koyré ressalta a relação de Galileu com o platonismo, expressa pela importância dada à razão e ao papel da matemática.”
“Galileu foi um fabricante de instrumentos. Entretanto, apesar de suas contribuições ao aprimoramento do telescópio serem reconhecidas, essa faceta tinha sido marginalizada na história que vigorou até o princípio da segunda metade do século XX. Na verdade, a imagem de Galileu como um cientista teórico, com semblante moderno, foi questionada nos anos 40 nos trabalhos de Edgar Zilsel, pensador austríaco que emigrou para os Estados Unidos fugindo da perseguição nazista. Segundo esse historiador e filósofo da ciência, de inspiração marxista, os mesmos avanços sociais que tiveram lugar na Europa entre os séculos XII e XVI ocorreram também no domínio tecnológico. As artes práticas teriam sido estimuladas pelas novas necessidades e inspirado uma confiança na continuidade dos avanços da tecnologia. O poder que os teóricos dos séculos XV e XVI experimentavam, uma vez que tinham se apropriado da literatura dos sábios da Antiguidade, era semelhante à sensação que os artesãos tinham diante das melhorias que haviam conseguido empreender por meio de ferramentas importantes para a organização da vida em sociedade.
Segundo a teoria que ficou conhecida como ‘tese de Zilsel’, entre 1300 e 1600 distinguem-se ao menos 2 estratos da organização social: intelectuais acadêmicos e artesãos qualificados. A estes vem se somar, em muitas regiões, um 3º grupo: o dos pensadores humanistas. Os professores e humanistas tinham certo desprezo pelas artes mecânicas e pelos trabalhos manuais. Por outro lado, os artesãos qualificados, que incluíam artistas-engenheiros, agrimensores, construtores de instrumentos musicais, náuticos e de guerra, eram mestres na prática da experimentação. Tratava-se de dois mundos separados: os últimos, tidos como plebeus, não tinham treinamento intelectual teórico; e aos primeiros, integrantes das classes mais altas, faltava um contato com a experiência prática e com as possibilidades dos instrumentos. A atividade intelectual era derivada da estrutura hierárquica da sociedade. Logo, os dois componentes do método científico estavam separados por uma barreira social. Somente quando os preconceitos começaram a ruir, por volta de 1600, eles puderam unir seus conhecimentos e experiências. Os trabalhos de Galileu devem ser analisados nesse contexto de desenvolvimento de uma sociedade capitalista.”
“Histórias mais recentes, como a exposta por M. Valleriani em Galileo Engineer, já aceitam a importância dada à prática na época e procuram ir além da tese de Zilsel, analisando como a aproximação desses 2 mundos influenciou a própria física de Galileu. Mas, antes de abordar essas novas tentativas, faremos um brevíssimo resumo do percurso de Galileu como pensador.”
“se temos dois volumes iguais de água e de madeira, o volume de água será mais pesado, logo, não podemos fazer o volume de madeira submergir. Essa explicação se opõe à teoria das causas aristotélicas, segundo a qual o movimento não se dá por qualidades de cada corpo e sim por uma causa única, o peso, que é como uma força que interage com a ação de um meio.”
“Entre 1613 e 1615, Galileu escreveu algumas cartas que ficaram conhecidas como Lettere copernicane (Cartas copernicanas), nas quais afirma que algumas passagens da Bíblia deviam ser interpretadas à luz do sistema heliocêntrico, para o qual ele não tinha ainda provas científicas conclusivas.”
“Dialogo sopra i due massimi sistemi del mondo tolemaico e copernicano (Diálogo sobre os dois principais sistemas do mundo ptolomaico e copernicano), finalizado em 1630 e publicado em 1632, no qual voltou a defender o sistema heliocêntrico. Essa obra foi decisiva no processo da Inquisição montado contra ele.
Em 1638, foram publicados os seus Discursos e demonstrações matemáticas sobre duas novas ciências. Trata-se do primeiro tratado sobre a cinemática e a dinâmica dos movimentos nas proximidades da superfície da Terra. Redigido na forma de diálogos, seguia a tradição grega que se tornara comum no Renascimento. Seus 3 interlocutores são: Salviati (que representa o próprio Galileu), Simplício (que defende a filosofia e a física de Aristóteles) e Sagredo (personagem prático, de mentalidade aberta, que atua como uma espécie de árbitro entre as duas posições em confronto) [SSS]. O livro é constituído basicamente por 4 ‘jornadas’. A primeira é uma introdução às ‘duas novas ciências’: a resistência dos materiais e o estudo do movimento. A segunda trata da estática e desenvolve as idéias e os modelos de Galileu sobre a resistência dos materiais. Nas duas últimas ‘jornadas’, discutem-se o movimento acelerado e as leis que regem o movimento dos projéteis.”
SÃO GALILEU (O PADROEIRO DOS CIENTISTAS DA BOMBA “A”): “No final do século XV, surgiram armas de artilharia pesada ligadas a novas estratégias de defesa e, na primeira metade do século XVI, trabalhos como os de Tartaglia debruçavam-se no estudo do movimento dos projéteis. Se analisarmos o aprendizado de Galileu como artista-engenheiro (entre 1584 e 1589) e o trabalho que realizou durante sua estada em Pádua (entre 1592 e 1610), veremos que devotou tempo considerável a pesquisas sobre guerra. Ele concebeu instrumentos matemáticos para uso militar e abriu uma oficina para construí-los.” “Quando conseguiu aumentar o alcance do telescópio, em 1609, estava envolvido justamente nessa economia de artefatos e sua idéia inicial não era desenvolver um instrumento astronômico para comprovar o heliocentrismo, e sim fornecer uma nova ferramenta militar à Marinha de Veneza.”
“Segundo Valleriani, o estudo da queda livre foi diretamente influenciado pela pesquisa de Galileu sobre a trajetória de projéteis, uma questão fundamental para a balística da época. O modelo central analisado por ele é o movimento de queda, livre ou sobre um plano inclinado, de modo que a distância de um corpo em relação ao ponto inicial aumenta com o quadrado do tempo transcorrido. Se esse movimento de queda é superposto a um movimento uniforme horizontal, obtemos a trajetória parabólica de um projétil.”
“Na época da publicação de Discursos e demonstrações matemáticas sobre duas novas ciências, a Geometria de Descartes já havia sido escrita, mas Galileu não estava a par desse trabalho.
No Diálogo, publicado antes dos Discursos, encontramos também uma tentativa de representar 2 magnitudes diferentes, no caso, o tempo e a velocidade, como pontos definidos a partir de 2 eixos coordenados. Mas, apesar da utilização engenhosa dos diagramas na representação do movimento, é um exagero considerar Galileu o fundador da representação em coordenadas, pois o passo fundamental das justamente denominadas ‘coordenadas cartesianas’ depende da utilização da álgebra. Como no plano de Oresme, não são usadas ferramentas algébricas na demonstração de Galileu.”
“Segundo Bacon, em vez da lógica aristotélica, o método indutivo podia ser mais frutífero para a enunciação de novas verdades científicas. Bacon não chegou a ver a primeira edição de uma de suas obras mais conhecidas, Nova Atlântida, publicada somente pouco depois de sua morte, ocorrida em 1626. Esse livro trata de uma localidade imaginária, marcada pela prosperidade e pela intervenção do homem na natureza.” “Está para além do escopo deste trabalho estudar as influências de Bacon sobre Descartes, entretanto, ainda que a obra de Bacon não tenha angariado popularidade imediata, a crítica à velha lógica e os esforços para encontrar novos métodos para a enunciação de verdades, presentes no Novum organum, foram apreciados por matemáticos como o padre Marin Mersenne e o próprio Descartes.”
A ASCENSÃO DOS EMPIRISTAS: “Em um texto de 1623, Il saggiatore, Galileu já descrevia a operação necessária ao estudo quantitativo dos fenômenos. Para conhecer uma matéria ou substância corporal seria preciso concebê-la como algo limitado, dotado de uma forma, ocupando um certo lugar em um dado momento, em movimento ou imóvel, em contato com outro corpo ou isolada, simples ou composta. Não importa se essa matéria era branca ou vermelha, amarga ou doce, com cheiro bom ou ruim. Para Galileu, essas qualidades deviam ser abstraídas em prol de uma descrição quantitativa.”
“Refletindo mais atentamente, pareceu-me por fim óbvio relacionar com a Matemática tudo aquilo em que apenas se examina a ordem e a medida, sem ter em conta se é em números, figuras, astros, sons, ou em qualquer outro objeto que semelhante medida se deve procurar; e, por conseguinte, deve haver uma ciência geral que explique tudo o que se pode investigar acerca da ordem e da medida, sem as aplicar a uma matéria especial: esta ciência designa-se não pelo vocábulo suposto, mas pelo vocábulo já antigo e aceito pelo uso de Matemática universal (Mathesis universalis) porque esta contém tudo que contribui para que as outras ciências se chamem partes da Matemática.” Descartes, Regras para a direção do espírito
CÉTICOS RACIONALISTAS: “Como afirma Barbin, a realidade é matemática porque foi tornada matematizável por separação, por triagem. Para Descartes, as deduções lógicas que permitem passar de uma proposição a outra devem ser substituídas por relações entre coisas quantificáveis, traduzidas por equações (igualdades entre quantidades). Quanto mais nos distanciamos das quantidades, mais o conhecimento toca o obscuro, podendo induzir a erro. Não podemos confiar nas aparências, no que acreditamos ser verdadeiro pelo testemunho dos sentidos. Poderia existir, como postula Descartes, um gênio maligno que faz com que estejamos enganados sempre que acreditamos ver, ou testemunhar, um certo fenômeno. Por isso é preciso duvidar sempre. Nesse quadro de incertezas, como obter uma certeza?”
“Se tomamos um pedaço de cera sabemos que ele possui certo tamanho, certa forma, certa cor, um cheiro, uma temperatura; e se batemos nele, podemos até ouvir um som. Mas o que acontece quando acendemos uma chama sobre essa cera? Evidentemente ela perderá todas essas propriedades. Por que então podemos, ainda assim, continuar a chamar de ‘cera’ o que resta? O que há de estável que permanece após essas profundas transformações? Descartes afirma que há algo que resta, chamado por ele de ‘extensão’, e que não diz respeito nem à matéria nem à forma [Não diz respeito à forma? Isso é bem estranho!], ou seja, não se identifica com o espaço ocupado pela cera.”
“Em 1626, Descartes freqüentou o círculo de pensadores que gravitavam em torno do padre Mersenne, em Paris, que se dedicava, entre outras coisas, a pesquisar problemas óticos ligados ao estudo do movimento dos raios luminosos. Esses trabalhos levaram Descartes a escrever Dióptrica, um dos ensaios publicados com o Discurso do método, ou seja, juntamente com a Geometria. Trata-se de um tratado de ótica que compreende uma teoria da refração da luz, e desde o início da obra percebe-se a proximidade de Descartes com os artesãos de instrumentos óticos.”
“já se sabia que as cônicas podiam ser usadas para construir lunetas e espelhos, bem como servir à relojoaria. Pesquisadores do círculo de Mersenne investigavam como transformar um raio luminoso cilíndrico em um feixe de cônicas, e a conseqüência disso para a geometria é que o problema das curvas óticas implicava a busca de curvas desconhecidas, ou seja, de curvas que realizassem certos efeitos óticos.
O que Barbin designa como ‘invenção do curvo’ é uma concepção geral das curvas existente na época que não se limitava ao estudo de curvas particulares, ampliando o universo dos objetos geométricos pela introdução de curvas que descrevem movimentos ou são expressas por equações algébricas. Em diversos problemas, tratava-se de procurar um objeto desconhecido que podia ser uma curva, em um sentido bem mais geral do que se considerava anteriormente.”
“A construção das ovais, que possuem a propriedade de fazer com que os raios de luz convirjam para um único ponto, mostra a utilidade instrumental de sua matemática no campo da ótica; mas a superioridade do método será afirmada com a resolução de um problema herdado dos antigos, cuja solução ainda não havia sido encontrada: o problema de Pappus, que estudaremos a seguir.”
“Se queremos resolver qualquer problema, primeiramente supomos que a solução já está efetuada e damos nomes a todas as linhas que parecem necessárias para construí-la. Tanto para as que são desconhecidas como para as que são conhecidas. Em seguida, sem fazer distinção entre linhas conhecidas e desconhecidas, devemos percorrer a dificuldade da maneira mais natural possível, mostrando as relações entre essas linhas, até que seja possível expressar uma única quantidade de dois modos. A isto chamamos uma Equação, uma vez que os termos de uma dessas duas expressões são iguais aos termos da outra.”
“Temos [pela 1ª vez] uma potência quadrada que não é associada a um quadrado, mas a um segmento de reta.” “Isso foi possível pela escolha de um segmento de reta arbitrário considerado ‘unidade’. A partir daí, o produto de 2 segmentos pôde ser interpretado como um outro segmento, e não mais necessariamente como a área de um retângulo.”
“Problema de Pappus
Encontrar o lugar geométrico de um ponto tal que, se segmentos de reta são desenhados desde esse ponto até 3 ou 4 retas dadas em ângulos determinados, o produto de 2 desses segmentos deve ser proporcional ao produto dos outros 2 (se há 4 retas) ou ao quadrado do 3º (se há 3 retas).
Pappus demonstrou que, no caso geral, a solução deve ser uma cônica. Descartes, inspirado por esse matemático grego, passou a considerar o problema para mais de 4 retas, o que dará origem a curvas de maior grau. Em uma forma simplificada, o problema consiste em: dadas 2n retas, encontrar o lugar geométrico de um ponto móvel tal que o produto de suas distâncias (não necessariamente em ângulo reto) a n das retas (em posições determinadas, com ângulos dados) é proporcional ao produto das distâncias às outras n retas.”
“atribuindo valores a y teremos equações do tipo x² = ±px ± q², para as quais a solução pode ser construída com régua e compasso (por meio dos métodos que
Descartes havia deduzido para a construção de raízes de equações quadráticas). Tomando sucessivamente infinitos valores para y, obtemos infinitos valores para x e, para cada par x e y, fica determinado um ponto C, o que permite desenhar a curva.”
“O QUE SÃO EQUAÇÕES INDETERMINADAS?
Há uma diferença de natureza entre as equações x² − 4x + 3 = 0 e x² + y² = 1. No primeiro caso, trata-se de encontrar o valor da quantidade desconhecida x, que, mesmo não sendo conhecida, pode ser determinada por uma das igualdades x = 3 ou x = 1. No segundo caso, x e y não possuem valores determinados, por isso dizemos que se trata de uma equação indeterminada. Podemos variar os valores de x, o que nos fará obter, de modo geral, diferentes valores para y. No exemplo, se x e y são números reais, o lugar geométrico dos pontos que satisfazem à equação é uma circunferência de raio 1. O papel do símbolo x muda também de um caso para o outro, por isso pensamos ser mais adequado dizer que, no primeiro caso, x é uma incógnita e, no segundo, uma variável.”
“A prática da arte analítica do final do século XVI e início do XVII envolvia numerosos estudos de problemas particulares, abordados com métodos heterogêneos que tinham em comum a utilização da análise por meio da ferramenta algébrica. A aplicação dos novos métodos à resolução de problemas geométricos não seguia uma norma bem-definida. Antes de Descartes, os diversos procedimentos de construção utilizados não tinham sido submetidos a uma ordenação nem a teorias unificadoras acerca de sua legitimidade. Sabia-se que o uso de métodos algébricos na análise envolvia a relação entre problemas, equações e construções, mas a natureza dessas relações não era bem-compreendida. Um dos objetivos da Geometria de Descartes era ordenar o domínio da resolução de problemas geométricos por meio da arte analítica, postulando um novo padrão de rigor e uma nova noção de exatidão para os procedimentos de construção.”
“Parece claro que se assumimos que a geometria é precisa e exata, enquanto a mecânica não é; e se pensamos a geometria como uma ciência que fornece um conhecimento geral das medidas de todos os corpos, então não temos mais o direito de excluir curvas mais complexas, bastando que elas sejam concebidas como curvas descritas por um movimento contínuo ou por vários movimentos sucessivos, cada um sendo completamente determinado pelos precedentes; pois desta forma um conhecimento exato da magnitude de cada um é sempre possível.”
“não se trata de um movimento qualquer dependendo do tempo. O escopo dos movimentos que podem ser considerados para gerar curvas é restrito e depende de critérios geométricos. As curvas consideradas ‘geométricas’ serão aquelas cujas coordenadas possuem necessariamente alguma relação com todos os pontos de uma reta, relação que pode ser expressa por meio de uma única equação.(*) Em seguida, as curvas serão classificadas pelo grau dessa equação, sendo o caso mais simples, de 2º grau, referente ao círculo, à parábola, à hipérbole e à elipse.
(*) Descartes só considera as curvas algébricas; as outras (que hoje chamamos transcendentes, como as trigonométricas e logarítmicas) deviam ser excluídas da geometria.”
“Vimos que o início do século XVII foi marcado por esforços de diversos matemáticos para recuperar as obras clássicas mencionadas por Pappus. Entre elas, uma das mais importantes eram as Cônicas, de Apolônio. O objetivo dos trabalhos iniciais de Fermat era exprimir os problemas geométricos de Apolônio na linguagem algébrica proposta por Viète. A geometria analítica de Fermat atingiu sua forma final por volta de 1635, mas esse bacharel em direito já estudava o assunto desde os tempos em que esteve em Bordeaux, antes de voltar para Toulouse. No final de 1636, ele enviou a Paris uma cópia de sua Introdução aos lugares geométricos planos e sólidos, quando iniciava uma correspondência com os matemáticos parisienses. Na época, Fermat não conhecia a Geometria de Descartes, mas sua obra também estabelecia uma correspondência entre lugares geométricos e equações indeterminadas. Logo no princípio da Introdução, ele propunha: sempre que em uma equação final duas quantidades desconhecidas são encontradas, temos um lugar geométrico e a extremidade de uma delas descreve uma linha, reta ou curva.”
“Quando os matemáticos próximos de Fermat tomaram conhecimento desses trabalhos, reagiram com ceticismo. Mesmo aqueles envolvidos na prática da ‘arte analítica’ eram tributários do estilo euclidiano de apresentação. Viète fez questão de deixar claro, na Introdução à arte analítica, que suas demonstrações algébricas podiam ser revertidas com o fim de obter um argumento sintético, apesar de já existirem trabalhos que indicavam um relaxamento em relação a esse tipo de demonstração. Na época, usar a análise algébrica sem demonstrações sintéticas era considerado deselegante, e quando Fermat apresentou suas pesquisas a Mersenne, em 1636, chegou a se desculpar, afirmando que seus resultados podiam despertar algum interesse ainda que não tivesse tido tempo de escrever as demonstrações. Ele pretendia apresentá-las depois, mas nunca chegou a fazer isso. Alguns historiadores, como Mahoney, observam que Fermat não se prendia muito às convenções da matemática clássica: estava interessado em seus problemas e na efetividade da arte analítica para tratá-los.”
“Foi a partir da publicidade obtida em torno da obra de Descartes que essa nova geometria tornou-se conhecida, obscurecendo o papel de Viète. Mesmo que a qualidade matemática dos métodos de Fermat seja equiparável à apresentada por Descartes, o uso da terminologia e da notação de Viète fez diminuir sua popularidade. Logo após um conhecer a obra do outro, iniciou-se uma controvérsia entre Descartes e Fermat que não tinha por objeto, contudo, a busca da prioridade dos métodos da nova geometria. Junto com a Introdução aos lugares geométricos planos e sólidos, Fermat havia enviado a Mersenne a tradução de Lugares geométricos planos, de Apolônio, e mais outro texto, de sua autoria, Méthode pour la recherche du maximum et du minimum et des tangentes aux lignes courbes (Método para determinar máximos e mínimos e tangentes a linhas curvas). Foi por essa obra que alguns matemáticos do círculo de Mersenne começaram a admirar Fermat, caso de Roberval, que ajudou a divulgar o talento desse matemático até então desconhecido.”
AH, O EGO! INVEJO, LOGO SOU! “Entre 1637 e 38, Fermat escreveu uma crítica à Dióptrica de Descartes, à qual tivera acesso de forma não-autorizada, por meio de um colega. Descartes ficou furioso, principalmente porque o trabalho ainda era inédito. Antes da publicação efetiva do Discurso do método (que compreendia a Dióptrica, além da Geometria), seu autor tomou conhecimento da geometria analítica de Fermat e de seu modo de encontrar máximos e mínimos, o que fez com que receasse que a obra de Fermat ofuscasse o brilho do seu novo método, que estava prestes a se tornar conhecido. Com a singularidade de sua abordagem, Descartes pretendia impressionar a intelectualidade francesa; e as críticas de Fermat, bem como suas inovações na geometria, atrapalhavam tal propósito. Depois de perceber que os métodos de Fermat estavam corretos, Descartes centrou seus ataques contra seu estilo, que abria mão de fornecer métodos gerais e sistemáticos. Assim, a habilidade do matemático de Toulouse resumia-se, para ele, à arte de resolver problemas.”
CAPÍTULO 6. Um rigor ou vários? A análise matemática dos sécs. XVII e XVIII
“No caso da noção de ‘função’, diversos escritos fornecem uma lista com a evolução das principais definições, do século XVII ao início do XX, de modo esquemático. Isso nos faz acreditar que teria havido um desenvolvimento linear durante o qual essas definições foram sendo aprimoradas até culminar com a versão rigorosa usada atualmente, baseada na linguagem dos conjuntos. Mas por que essas definições precisaram ser reformuladas? Quando elas se tornaram insatisfatórias e, principalmente, por que permaneceram satisfatórias durante tanto tempo?
A história do cálculo infinitesimal também recebe um tratamento retrospectivo. Apresentam-se diferentes técnicas que remontam aos paradoxos de Zenão, passando pelo método grego da ‘exaustão’ e pelos métodos de Cavalieri para calcular áreas até chegar a Leibniz e Newton.”
“Em sua história do cálculo, publicada originalmente em 1949, C.B. Boyer destaca a mudança de ponto de vista ocorrida em meados do século XVIII, quando se passou a rejeitar concepções geométricas e enfatizar métodos formais (cf. C.B. Boyer, The History of Calculus and its Conceptual Development). Essa tendência foi documentada mais tarde, e com mais detalhes, por outros historiadores, como H.J.M. Bos em ‘Differentials, higher-order differentials and the derivative in the Leibnizian calculus’.”
“função, número real e número complexo: É praticamente impossível compreender tais conceitos sem investigar o contexto em que apareceram, intimamente ligado às discussões sobre o cálculo infinitesimal e às transformações na concepção de rigor.” Que beleza, então, o ensino básico de matemática nas escolas!
“Em qualquer curso de cálculo infinitesimal, a definição de derivada é antecedida pela sentença: ‘Seja uma função y = f(x)’. Porém, o conceito de função só foi introduzido na matemática após o aprimoramento das técnicas diferenciais efetuado por Leibniz e Newton. Esse é mais um exemplo de que os conteúdos matemáticos que aprendemos não são organizados de modo cronológico. Fosse assim não poderíamos aprender funções, no 9º ano, sem algumas noções básicas sobre derivadas e integrais.
Até o advento do cálculo, a matemática era uma ciência das quantidades. No século XVII, o trabalho sobre curvas relacionava quantidades geométricas. Já a partir do século XVIII muitos matemáticos começaram a considerar que seu principal objeto era a função. Essa mudança foi descrita da seguinte forma por Jaques Hadamard, Le calcul fonctionnel: ‘O ser matemático, em uma palavra, deixou de ser o número: passou a ser a lei de variação, a função. A matemática não apenas foi enriquecida por novos métodos; foi transformada em seu objeto.’”
“A identificação entre função e expressão analítica defendida no século XVIII muitas vezes está mais presente na cabeça de nossos estudantes do que sua definição formal, em termos de conjuntos, proposta no século XIX.”
“A noção de rigor também tem uma história, e não há um padrão único que a matemática mais recente teria descoberto como universal, tornando as contribuições dos matemáticos anteriores somente um caminho em sua direção.”
“Para que a matemática pudesse se libertar dos padrões gregos, associados ao cânone euclidiano, pensadores do século XVII, incluindo Leibniz, defendiam suas práticas como uma arte da invenção, para qual não importavam tanto os critérios de demonstração e sim o que as ferramentas permitiam obter em termos de novidade”
“Veremos que o papel da análise matemática, bem como de sua algebrização, deve ser compreendido no contexto da institucionalização do ensino na França depois da Revolução de 1789.”
“A ciclóide é definida pelo movimento de um ponto P em uma circunferência que rola sobre uma superfície plana sem atrito. Quando a circunferência dá uma volta completa em um movimento da esquerda para a direita, o ponto P traça um arco de ciclóide, conforme se vê na Figura 1.”
“Para obter esse resultado, Roberval usou o método dos indivisíveis, que havia sido formulado pelo aluno de Galileu chamado Bonaventura Cavalieri, autor de um modo geométrico para calcular áreas publicado em 1635.”
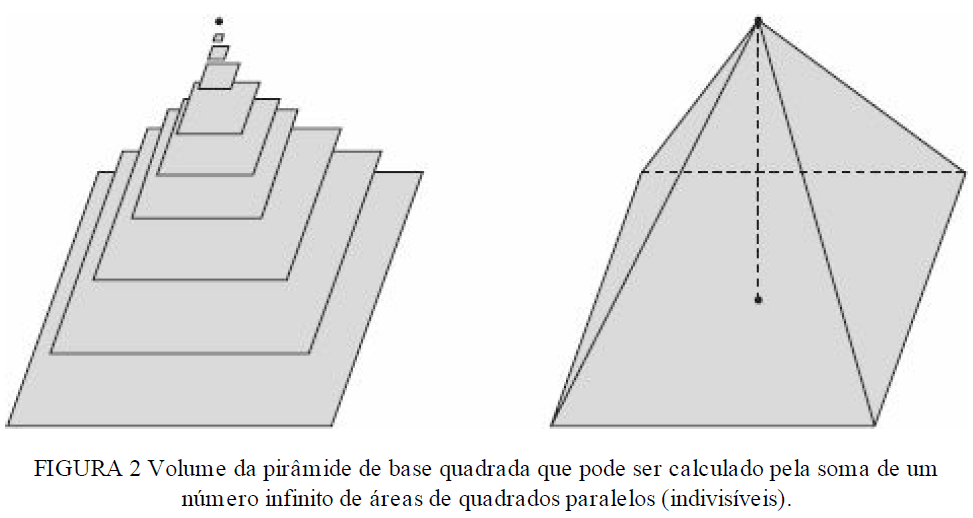
Surgiu, assim, uma nova maneira de calcular áreas por meio da aproximação de uma área por retângulos infinitamente finos, e essa ferramenta podia ser aplicada a qualquer figura curvilínea.”
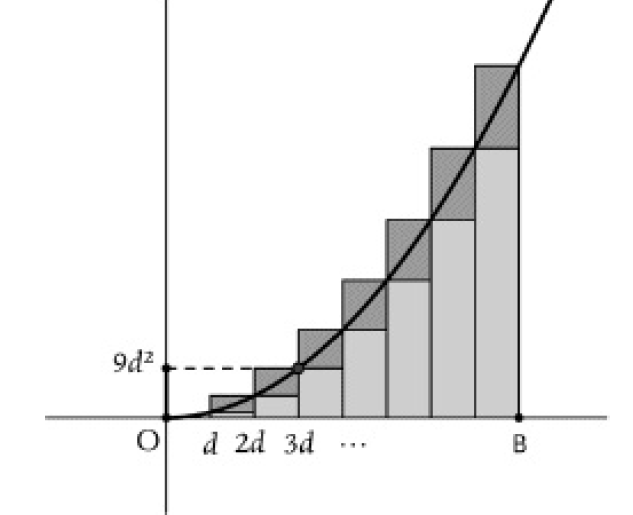
A = OB³/3 = x³/3
“Esse método se estende facilmente para outras curvas, distintas da parábola; basta que tenhamos uma equação que substitua as alturas dos retângulos. Para isso, é preciso conhecer a soma das m-ésimas potências dos n primeiros números naturais. Por volta de 1636, Fermat já sabia que, para n racional e diferente de −1, a área sob o gráfico de y = xn entre 2 pontos O e B (a uma distância a de O) é dada por an+1/n+1.
Há uma diferença fundamental entre essa técnica e o método de exaustão usado pelos gregos, entre eles Arquimedes, pois aqui não se usa nenhuma prova indireta para se chegar ao resultado final.” “O procedimento de dupla redução ao absurdo, usado pelos antigos geômetras, era indireto, ao passo que o novo método permite obter a área diretamente.”
“Pascal defendia seus procedimentos apelando para argumentos de inteligibilidade. O método dos indivisíveis parece não ser geométrico e pode até ser considerado um pecado contra a geometria, mas trata-se somente da soma de um número infinito de retângulos que difere da área por uma quantidade menor que qualquer quantidade dada. Para Pascal, os que não entendiam a razão desse procedimento possuíam, decerto, uma limitação ligada à falta de inteligência. [hahaha]” Tão pio em religião, tão pragmático em questões axiomáticas!
“Ao contrário da exposição sintética da geometria euclidiana, que apresenta uma construção sem nos permitir perceber como ela foi obtida, a associação de grandezas geométricas a quantidades algébricas exibe o caminho percorrido para se chegar ao resultado. No exemplo, ainda que se tenha partido de teoremas geométricos, o resultado final foi obtido por meio de uma manipulação algébrica. Essa via era considerada por Arnauld e por outros matemáticos do século XVII a mais natural, em contraposição ao método axiomático de Euclides.”
“Um dos primeiros a defender publicamente tal método foi o marquês de L’Hôpital, na obra que popularizou os métodos infinitesimais: Analyse des infiniments petits pour l’intelligence des lignes courbes (Análise dos infinitamente pequenos para a compreensão das linhas curvas), editada em 1696. No prefácio, L’Hôpital faz um histórico desse método, afirmando que Descartes foi o primeiro a deixar os antigos para trás, mas também cita Fermat, Barrow, Leibniz e Bernoulli.”
“Jean Prestet condenava, por exemplo, a ausência de uma explicação sobre as operações aritméticas expostas nos Elementos de Euclides, dizendo que essa obra era inútil para um aprendiz de matemática.” “No final do século XVII e início do XVIII, o grupo do filósofo cartesiano, padre e teólogo francês Nicolas Malebranche, do qual Prestet fazia parte, disseminou essa postura na Academia de Ciências de Paris, contribuindo, assim, para a modernização da matemática francesa.”
“Após ter estudado direito e filosofia, Leibniz participou, em 1672, de uma missão diplomática à corte de Luís XIV, na França, onde conheceu Christian Huygens. Antigo aluno de Descartes, Huygens trabalhava intensamente sobre séries e apresentou a Leibniz, até então praticamente ignorante em matemática, os trabalhos de Cavalieri, Pascal, Descartes, St. Vincent, J. Wallis e J. Gregory. Os métodos analíticos de Descartes e Fermat haviam motivado o estudo das propriedades aritméticas de séries infinitas na Inglaterra, sobretudo por Wallis, Gregory e Isaac Barrow. Esses pesquisadores resolviam com sucesso um grande número de problemas, como encontrar a tangente a uma curva, calcular quadraturas ou retificar curvas, e tiveram forte influência sobre Newton e Leibniz.
A maior novidade introduzida na matemática por Newton e Leibniz reside no grau de generalidade e unidade que os métodos infinitesimais adquiriram com seus trabalhos. Os matemáticos já tinham um enorme conhecimento sobre como resolver problemas específicos do cálculo infinitesimal, mas não se dedicaram a mostrar a generalidade e a potencialidade das técnicas empregadas. Além disso, esses problemas eram tratados de forma independente e as semelhanças entre os métodos não eram ressaltadas.”
“nos trabalhos do fim do século XVII, o conceito de curva recobria 3 aspectos: a curva como expressão algébrica, eventualmente infinita; a curva como trajetória de um ponto em movimento; e a curva como polígono com número infinito de lados. Essas três concepções foram essenciais no desenvolvimento dos métodos infinitesimais, e Leibniz teve papel central nessa mudança. Depois de ler a geometria de Descartes, em 1673, ele considerou seu método de tangentes restritivo. Além de ser complicado, o procedimento não se aplicava a uma grande quantidade de curvas. Uma das principais contribuições de Leibniz foi justamente estender o domínio das curvas para além das algébricas, vistas por Descartes como as curvas da geometria por excelência.”
“Com fórmulas simbólicas, Leibniz enunciou as regras para encontrar a derivada de somas, diferenças, produtos, quocientes, potências e raízes. Essas regras constituíam o algoritmo desse cálculo, que ele denominava diferencial.”
“Com isso também pretendia mostrar que novos métodos eram necessários para estudar relações entre grandezas que não podiam ser tratadas com a álgebra ordinária, caso da relação de uma curva com sua tangente ou sua normal. Entrava-se, portanto, em um novo domínio da relação entre quantidades, o que, como veremos, contribuirá para o surgimento da idéia de função como relação entre quantidades.”
“Em um artigo de 1694, ‘Considerações sobre a diferença que existe entre a análise ordinária e o novo cálculo dos transcendentes’, ele afirmou que seu método fazia parte de uma matemática geral que tratava do infinito e que, por isso, ele seria necessário se quiséssemos usar a matemática na física, uma vez que o infinito está presente na natureza.”
“Um exemplo paradigmático é o estudo do pêndulo, feito por Huygens, que servia à relojoaria e envolvia a análise detalhada da ciclóide. Depois dos exemplos propostos por seu mentor, Huygens, Leibniz também foi motivado por estudos físicos desenvolvidos por Johann Bernoulli.”
“PÊNDULO DE HUYGENS
No pêndulo simples, o tempo de oscilação (período) varia de acordo com a amplitude da mesma. No caso de pequenas oscilações, o período não se altera. Huygens construiu um pêndulo cujo período não se alterava com a amplitude da oscilação, ou seja, ele construiu um pêndulo isócrono. A importância de se construir um pêndulo com tal característica residia na possibilidade de obter cronômetros mais precisos para os relógios, principalmente cronômetros marítimos, pois o balanço dos navios alterava as amplitudes das oscilações.”
Foi Huygens o pai do opressor tempo moderno?
“Dadas certas propriedades de uma curva, que podem ser propriedades infinitesimais, expressas como uma relação entre as coordenadas da curva, busca-se a curva. Um exemplo famoso é o da braquistócrona, proposto em 1696 por Johann Bernoulli. O desafio consistia em, dados dois pontos situados em um plano vertical, determinar o caminho entre eles ao longo do qual um corpo desce, pela ação da gravidade, no menor período de tempo. O problema atraiu a atenção de vários matemáticos, como Leibniz, Newton, L’Hôpital, Tschirnhaus e Jakob Bernoulli.”
“Segundo Leibniz, sua primeira inspiração para a invenção do cálculo infinitesimal veio com a leitura do ‘Tratado dos senos do quarto de círculo’, escrito por Pascal em 1659. Baseado no modo como Pascal demonstrava um resultado sobre quadraturas, Leibniz criou o seu ‘triângulo característico’, uma ideia geral da qual se serviu diversas vezes e que nos ajuda a entender como Leibniz concebia o cálculo.”
“como é possível entender e justificar a razão entre 2 quantidades que deixaram de existir? Esse tipo de consideração gerou inúmeras controvérsias sobre o estatuto dessas ‘quantidades infinitamente pequenas’. Alguns estudiosos viram nas grandezas não-atribuíveis de Leibniz um apelo a certas quantidades que estão entre a existência e o nada.”
Leibniz “inventou” a equação diferencial ao chegar a seu dy/dx = 2x.
“tomemos um primeiro tipo de relação, as razões, sendo que para Leibniz razão era diferente de fração. Para ele, uma fração era a divisão de 2 números, logo, era 1 quantidade obtida pela divisão de 2 quantidades. Isto é, mesmo que seja verdade que as duas frações +1/-1 = -1/+1 são iguais, frações não são o mesmo que razões, ainda que estas sejam expressas por aquelas.”
“Leibniz não chegou a enunciar desse modo, pois não propôs um conceito de função. Pode-se argumentar, no entanto, que ele já admitia que as quantidades devem estar em relação. Essa conclusão sugere que não é relevante investigar a justificativa dos infinitesimais, sendo mais instrutivo ressaltar que eles sempre aparecem em relação.” “Logo, essa relação não pode ser entendida como um quociente entre 2 quantidades infinitamente pequenas, não-atribuíveis ou evanescentes, o que seria contraditório com a impossibilidade de dividir 0 por 0.”
“A riqueza da notação proposta por Leibniz é justamente ter introduzido o operador d, separando-o, ao mesmo tempo, da quantidade x à qual ele se relaciona e indicando a ligação com essa quantidade.
Como afirma Bos, não é sobre a diferencial, como objeto, que se funda o cálculo leibniziano, mas sobre a idéia de diferenciabilidade.¹ Daí a importância de se introduzir a expressão ‘diferenciar em relação a’, indicando a percepção clara de que a diferenciação é a noção central do cálculo, e não as diferenciais.”
¹ O Tite adoraria!
“No final da década de 1660, isto é, antes mesmo do encontro entre Leibniz e Huygens, Newton já empregava procedimentos infinitesimais e, no início dos anos 1670, reformulou esses algoritmos na linguagem de ‘fluentes’ e ‘fluxões’.”
“O livro Philosophiæ naturalis principia mathematica (Princípios matemáticos da filosofia natural), maior obra de Newton, não contém desenvolvimentos analíticos. Os resultados são apresentados na linguagem da geometria sintética. Esse formalismo euclidiano era considerado mais adequado para expor uma nova teoria. Como vimos, tal ponto de vista não era compartilhado por Leibniz, que, influenciado pelo contexto francês, pretendia fundar um cálculo universal baseado em ferramentas e algoritmos que deveriam constituir uma arte da invenção.”
“Leibniz promoveu sua teoria e o uso dos infinitesimais como uma maneira de descobrir novas verdades. Já Newton, para fazer com que sua teoria fosse aceita, se preocupou em garantir uma continuidade histórica entre seus métodos e os dos antigos.
Essa diferença se reflete no estilo e na regularidade das publicações de ambos. Uma singularidade de Leibniz reside justamente no fato de publicar sem grandes receios de cometer equívocos, podendo rever suas posições em outros artigos. Por exemplo, em relação às justificativas para os métodos infinitesimais, algumas das quais já descrevemos, Leibniz possuía diferentes versões, muitas contraditórias entre si, não se importando tanto em manter uma coerência. Newton, ao contrário, talvez ciente da fragilidade dos novos procedimentos infinitesimais, trabalhava bem seus argumentos antes de torná-los públicos e considerava o padrão da geometria grega mais adequado para transmitir suas idéias.”
“A partir de 1696, houve uma mudança importante no funcionamento da pesquisa matemática, pois, sob influência do grupo de Malebranche, a Academia passou a se organizar em classes, instaurando, pela 1ª vez, uma classe de matemáticos com postos de trabalho remunerados que atuavam somente como pesquisadores.” Cf. G. Schubring, ‘Aspetti istituzionali della matematica’
“No caso do cálculo, a Academia se dividia entre um grupo mais tradicional, que declarava a superioridade dos métodos convencionais (incluindo Fermat e Huygens), e outro que defendia os novos métodos. Os ataques se dirigiam, principalmente, ao uso de quantidades infinitamente pequenas por L’Hôpital, mas também ao postulado relativo à definição da igualdade, admitido por ele e por Johann Bernoulli, com inspiração leibniziana.”
“Na Inglaterra, o início do século XVIII testemunhou diversas críticas às quantidades infinitamente pequenas e aos métodos do cálculo. Uma das mais conhecidas foi formulada pelo filósofo George Berkeley, que publicou, em 1734, uma obra com um título que traduzimos para o português como: O analista ou um discurso endereçado a um matemático infiel. Na qual é examinado se o objeto, os princípios e as inferências da análise moderna são concebidos de um modo mais distinto, ou deduzidos de um modo mais evidente, do que mistérios religiosos e questões de fé.¹ Berkeley enumerava diversas definições e técnicas do cálculo que eram paradoxais e contradiziam a intuição, como a de eliminar quantidades infinitamente pequenas nas contas.”
¹ Que bobagem. Sabe de nada, inocente!
“Tal proposta [do inglês McLaurin] influenciou o francês Jean le Rond d’Alembert a defender a substituição das quantidades infinitamente pequenas pelo método de limites, permitindo, contudo, a intervenção da álgebra.” “em sua acepção moderna, o limite é uma noção estática e não dinâmica (entendido como um número do qual é possível se aproximar indefinidamente).”
“Essa definição é apresentada no verbete Différentiel, publicado em 1751 na Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers, de d’Alembert e Diderot. » Imaginei
“A ENCICLOPÉDIA DE DIDEROT E D’ALEMBERT
A famosa Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers foi publicada na França entre 1750 e 1772, por Jean le Rond d’Alembert e Denis Diderot. Compreende 33 volumes e 71.818 artigos e contou com contribuições dos mais destacados personagens do Iluminismo, como Voltaire, Rousseau e Montesquieu. Trata-se também de um vasto compêndio das tecnologias do período, em que são descritos os avanços da Revolução Industrial inglesa e da ciência da época.”
“Outras tentativas de elaborar o conceito de limite se sucederam nas décadas seguintes. Um exemplo da proeminência dessa discussão foi o prêmio oferecido, em 1784, pela Academia de Berlim para quem rejeitasse os infinitamente pequenos. O trabalho vencedor usava a linguagem dos limites. Ainda que muitos desses trabalhos tenham sido escritos na França, a defesa dos limites se encaixava mais no estilo inglês, influenciado por Newton. Ao passo que na Inglaterra os argumentos matemáticos associavam-se à mecânica, na França era mais comum apelar para a algebrização dos conceitos.”
“Diferentemente do que as narrativas tradicionais sugerem, o desenvolvimento das idéias fundamentais do cálculo não se deu no interior da matemática, como consequência dos trabalhos de uma comunidade imbuída em aperfeiçoar as lacunas formais de modo cumulativo. Durante os séculos XVII e XVIII, os métodos infinitesimais se inseriam em um domínio amplo que incluía não só a matemática, mas também a filosofia e a física. Além disso, as discussões acerca de sua natureza e legitimidade são inseparáveis do ambiente institucional em que aconteciam.”
“O que é uma variável? Como é possível representar simbolicamente uma variável? A noção de variável só foi introduzida formalmente no século XIX. Um passo fundamental para se chegar a esse conceito foi o nascimento da física matemática e a representação simbólica de uma quantidade desconhecida, proposta inicialmente por Viète mas desenvolvida no século XVII.”
“DEFINIÇÃO DE FUNÇÃO NO CONTEXTO ESCOLAR
A definição de função encontrada com mais frequência nos livros de ensino médio é:
Dados dois conjuntos X e Y, uma função f : X → Y é uma regra ou que diz como associar a cada elemento x ∈ X um elemento y = f(x) ∈ Y. O conjunto X chama-se domínio e Y é o contradomínio da função.” Não ajudou em nada!
“O estudo da variação por meio de leis matemáticas se deve em grande parte ao desenvolvimento da física pós-Galileu. A idéia de uma variação em função do tempo é fundamental em seus trabalhos, onde já encontramos uma certa noção de função no sentido de uma associação entre 2 grandezas que variam, dada por uma proporção geométrica. Uma função pode ser vista justamente como uma relação entre 2 grandezas que variam.”
“Apesar de terem pesquisado inúmeras relações funcionais, Leibniz e Newton não explicitam o conceito de função em suas obras. A falta de um termo geral para exprimir quantidades arbitrárias, que dependem de outra quantidade variável, motivou a definição de função, expressa pela primeira vez em uma correspondência entre Leibniz e Johann Bernoulli. No final do século XVII, Bernoulli já empregava essa palavra relacionando-a indiretamente a ‘quantidades formadas a partir de quantidades indeterminadas e constantes’. Tal concepção é a mesma que temos em mente quando associamos uma função à expressão f(x) = x + 2, por exemplo. Temos aí uma quantidade indeterminada x, que é suposta variável, e uma constante, no caso, 2.
Em uma resposta a Bernoulli, redigida em 1698, Leibniz discute qual seria a melhor notação para uma função. Nessa época, ele já havia introduzido os conceitos de constante e de variável, que se tornaram populares com a publicação do primeiro tratado de cálculo diferencial, por L’Hôpital em 1696. A definição explícita da noção de função com base nessa perspectiva só começou a ser delineada alguns anos mais tarde, em um artigo de Bernoulli apresentado em 1718 à Academia de Ciências de Paris em que ele diz o seguinte:
Definição. Chamamos função de uma grandeza variável uma quantidade composta, de um modo qualquer, desta grandeza variável e de constantes.
No mesmo artigo, ele usa a letra grega φ para representar a ‘característica’ da função, ou seja, o nome da função, escrevendo o argumento sem os parênteses: φx. Bernoulli não diz mais nada sobre o modo de constituir funções a partir da variável independente, mas o que ele tem em mente são as expressões analíticas de curvas.
Os primeiros passos para que o cálculo infinitesimal pudesse ser reconstruído com base na análise algebrizada foram dados por um pupilo de Johann Bernoulli, Leonard Euler. Apesar dessa proximidade entre eles, os livros de ambos diferem bastante em estilo. Ao passo que o primeiro privilegiava problemas geométricos e mecânicos (como vimos no caso da braquistócrona), o segundo pretendia se restringir à análise pura, sem recorrer a figuras geométricas para explicar as regras do cálculo. Foi com Euler que o cálculo passou a ser visto como uma teoria das funções, tidas como algo diferente de curvas. A idéia de que a análise matemática é uma ciência geral das variáveis e de suas funções exerceu grande influência sobre a matemática do século XVIII, a partir da publicação de sua Introductio in analysin infinitorum (Introdução à análise infinita), editada em 1748.”
“Uma quantidade variável compreende todos os números nela mesma, tanto positivos quanto negativos, inteiros e fracionários, os que são racionais, transcendentes e irracionais. Não devemos excluir nem mesmo o zero e os números imaginários.”
“Nessa época, supunha-se, implicitamente, que todas as funções pudessem ser escritas como uma série de potências da forma A + Bz + Cz² + Dz³+ …, ainda que fosse preciso considerar expoentes dados por qualquer número (e não apenas por números inteiros).”
“A profissão de fé dos matemáticos da época, que identificavam a função à sua expressão analítica, começou a ser questionada ainda no século XVIII, no contexto de um problema físico que faria intervir uma definição mais geral de função. Trata-se do ‘problema das cordas vibrantes’, que estuda as vibrações infinitamente pequenas de uma corda presa por suas extremidades. Uma corda elástica com extremidades fixas 0 e l é deformada até uma certa forma inicial; em seguida a soltamos. A corda começa a vibrar e o problema em questão é determinar a função que a forma da corda descreve em um instante t.”
“Já era sabido, na época, que os sons musicais, em particular os gerados pelas vibrações de uma corda, são compostos de freqüências fundamentais e de harmônicos. Essas vibrações podem ser expressas, portanto, como somas de funções trigonométricas, que são periódicas. Baseado nessa evidência, Daniel Bernoulli [filho de Johann] afirmou que a posição inicial de uma corda vibrante pode ser representada por uma série infinita de termos trigonométricos, que deve ser considerada tão geral quanto uma série de potências. Isso implica que uma função qualquer possa ser representada por uma série trigonométrica, mas Daniel Bernoulli estava mais interessado no problema físico e não chegou a propor uma nova definição de função com base nessa hipótese.”
“Tais funções eram denominadas descontínuas. A continuidade de Euler era uma noção muito distinta da atual, pois se relacionava à invariabilidade da expressão analítica que determina a curva. Se a curva era expressa por apenas uma equação em todo o domínio dos valores da variável, ela era contínua. Ela era descontínua se, ao contrário, fosse necessário mudar a expressão analítica que exprime a curva quando passamos de um domínio a outro das variáveis.”
“O problema das cordas vibrantes permaneceu confinado a tratados acadêmicos e não chegou a ser apresentado em livros-textos até o final do século XVIII. Do mesmo modo, o debate sobre o conceito de função não teve muita repercussão nesse século e definições mais gerais só surgiriam bem mais tarde.”
“É intrigante, por exemplo, que a história da algebrização da análise salte de Euler a Lagrange diretamente, uma vez que o primeiro não atuava na França. O citado livro de Gert Schubring foi o primeiro estudo histórico a focar os fenômenos de recepção e circulação dos escritos relacionados à análise no século XVIII. Apesar de a obra de Schubring abordar diferentes contextos nacionais, nos restringiremos à parte que remete à situação francesa, uma vez que nosso objetivo é bem mais específico: entender como, entre Euler e Lagrange, a análise algebrizada se tornou uma abordagem hegemônica.”
“A matemática e a química, sob a égide do método analítico, tornaram-se as disciplinas principais, responsáveis por disseminar os ideais de racionalidade então valorizados. Muitos matemáticos importantes viviam na França, como Lagrange, Laplace, Legendre e Monge, mas não tinham a função de ensinar. Na época pré-revolucionária, a instrução matemática ocupava um lugar marginal e carecia de professores qualificados. Essa disciplina constava do currículo do último nível do Collège (instituição de ensino secundário), fora do alcance da maioria dos alunos, que saíam da escola antes de atingir esse nível. A partir de 1750, foi estabelecido um segundo sistema educacional nas escolas militares que valorizava a matemática e atraía estudantes hábeis, porém, o recrutamento de alunos só abrangia a nobreza.”
“Depois da Revolução Francesa, alterou-se significativamente o perfil da sustentação financeira da pesquisa científica, até então beneficiada pela benevolência de patronos e reis. Os novos cientistas – pertencentes a uma classe média crescente – precisavam de suporte institucional, o que impulsionou a criação de novos postos de trabalho. Além disso, a idéia de que a formação científica podia ser útil à nação era cada vez mais aceita, tanto para a expansão da indústria como para o aperfeiçoamento da força militar, consciência que levou à criação de novas escolas e departamentos científicos. Em 1794, foi fundada a École Polytechnique, dedicada à formação de engenheiros e cientistas. Foi nesse contexto que Lagrange e Lacroix produziram livros-textos que se tornaram ferramentas cruciais para o ensino superior da matemática, formando gerações de matemáticos de peso, como o próprio Cauchy. Essas instituições públicas geraram uma inédita padronização do currículo que tinha no método analítico, praticado pela matemática e pela química, seu principal elemento. No contexto mais geral, na tradição do racionalismo, esse método já havia sido defendido pelo filósofo iluminista francês Étienne Bonnot de Condillac. Na matemática, a abordagem algébrica da análise podia vencer o conceito sintético (geométrico) das quantidades infinitamente pequenas.
Especialmente depois da queda de Robespierre, em 1794, um grupo de filósofos chamados idéologues (ideólogos) passou a determinar a política para a educação e a ciência. Depois dos ataques de Arnauld e Prestet aos métodos sintéticos de Newton, as críticas foram renovadas por esse grupo, que assumiu o programa dos malebranchistas e instituiu o método analítico como orientação predominante. Em um jornal dos idéologues publicado em 1794, lemos que ‘esse método deve ser, sem dúvida, fundado na análise … é somente por meio da análise que podemos penetrar com segurança no santuário da ciência’. O método analítico permitia descobrir novas verdades, ao passo que o sintético era longo e obscuro. A química também passou a operar com símbolos, e Lavoisier se baseou na filosofia analítica de Condillac para desenvolver seus trabalhos. Essa possibilidade de expressá-la em uma linguagem simbólica permitiu novas descobertas, provando a fecundidade da análise.”
“A recepção de Euler seguiu um curso contraditório ao papel atribuído a ele pela historiografia hoje, conforme nos mostra Schubring. Um número considerável de matemáticos lia seus trabalhos, em diferentes países, mas a maioria adotava somente alguns de seus resultados pontuais e não suas posições sobre os fundamentos da matemática. Euler não tinha relação com um sistema de ensino e suas obras eram direcionadas para um público mais acadêmico.”
“O curso inaugural de análise da École Polytechnique foi ministrado em 1795 por Gaspard Riche de Prony, engenheiro que tinha grande estima pela matemática. Apesar de seu curso, que foi publicado mais tarde, dedicar-se à análise aplicada à mecânica, ele se baseava, fundamentalmente, nos 2 primeiros capítulos da Introductio de Euler e adotava seus métodos e sua notação. Como consequência, seu texto é o primeiro na França a defender o conceito de função como objeto central da análise. O rompimento com a tradição se exprimia pela exclusão dos infinitamente pequenos.
A radicalidade de um outro movimento, capitaneado por Lagrange, se revela já no título de sua principal obra, publicada em 1797: Théorie des fonctions analytiques, contenant les principes du calcul différentiel, dégagés de toute considération d’infiniments petits, d’évanouissants, de limites et de fluxions, et réduits à l’analyse algébrique des quantités finies (Teoria das funções analíticas, contendo os princípios do cálculo diferencial, livres de qualquer consideração de infinitamente pequenos, evanescentes, limites e fluxões, e reduzidos à análise algébrica de quantidades finitas). Vemos aí uma vontade explícita de liberar a matemática das noções ambíguas de infinitamente pequenos e quantidades evanescentes, usadas por Leibniz, bem como das ‘fluxões’, quantidades variáveis usadas por Newton.
Lagrange fazia parte de uma segunda geração de analistas do século XVIII. Iniciou sua atividade nos anos 1770, quando já se preocupava com a questão dos fundamentos. Contudo, seu programa de algebrização dos métodos da análise só foi construído nos anos 1795-6, durante seus cursos de análise na École Polytechnique, quando as diferenciais passaram a ser definidas diretamente pela expansão de uma função em séries.”
“Lagrange criticou até mesmo algumas concepções de d’Alembert e Euler sobre os fundamentos. A função era dada por uma fórmula analítica finita, mas que podia ser representada por uma série de potências, como a descrita acima, que já tinha sido definida pelo inglês B. Taylor no início do século XVIII.”
“Desde os primeiros anos da École Polytechnique, a produção de livros-textos se tornou uma atividade significativa, uma vez que o conhecimento não se destinava mais somente às classes privilegiadas. Os livros sobre cálculo diferencial e integral tinham em comum a rejeição dos infinitamente pequenos e a defesa da concepção algébrica. Ainda em 1797, foi publicado o 1º volume de um livro de S.F. Lacroix, Traité du calcul différentiel et du calcul integral (Tratado do cálculo diferencial e integral), que contribuiu para difundir as novas ideias sobre a análise. Os 2 outros volumes saíram em 1798 e 1800. Em 1803, essa obra ganhou uma versão resumida, voltada para o ensino, reeditada várias vezes na França e traduzida em outros países.” “O uso do símbolo f para representar funções em geral também foi proposto nesse tratado.”
“Na sua Méchanique analytique (Mecânica analítica), de 1788, Lagrange já afirmava que a mecânica deve ser vista como uma parte da análise matemática, podendo prescindir de figuras ou de qualquer consideração geométrica. Ou seja, a análise matemática, identificada à análise algebrizada, pode se aplicar à geometria ou à mecânica, mas deve ser cultivada como um ramo distinto, com seus próprios fundamentos.”
“o problema original do cálculo, que era analisar matematicamente a variação sobre curvas, foi dando lugar ao estudo de fórmulas. Como a álgebra, a análise lidava com fórmulas e seus teoremas eram provados por meio de cálculos com essas fórmulas.”
“Essa confiança no formalismo decorria do sucesso dos métodos analíticos, e a generalidade da matemática, uma qualidade cara aos analistas, era assegurada pela generalidade dos métodos algébricos. Isso significa dizer que esses métodos operavam sobre objetos algébricos e sua generalidade era derivada da generalidade das fórmulas da álgebra. Logo, se uma demonstração era feita por meio de tais fórmulas, o resultado era admitido como válido em geral. Não havia sequer a necessidade de tecer especulações associadas ao domínio da aplicação das técnicas.
Essa crença na ‘generalidade da álgebra’ será criticada no século XIX, inicialmente por Cauchy. As pesquisas que ajudaram a desenvolver uma nova visão sobre o cálculo diferencial durante esse século tinham como motivação, segundo alguns historiadores, fundar a matemática sobre bases rigorosas. Essa interpretação pressupõe que os analistas do século XVIII não se importavam com o rigor de seus trabalhos. Mas Euler e Lagrange, só para dar 2 exemplos, foram responsáveis justamente por transformar o cálculo diferencial e integral de Leibniz e Newton com o fim de liberar esse cálculo de argumentos injustificados. Dito de outro modo, ao procurar fundar o cálculo em bases mais sólidas e esclarecer seus conceitos fundamentais, diversos matemáticos do século XVIII tinham na busca do rigor sua motivação.”
“No século XIX, no entanto, a noção de função será discutida, em um primeiro momento, com relação a um problema físico: o estudo da propagação do calor. O programa de ensino e o corpo de professores da École Polytechnique foram expandidos em 1796 e criou-se um curso de análise algébrica como introdução ao cálculo, já que, do ponto de vista da escola, não se podia confrontar os alunos diretamente com as ferramentas desse campo da matemática – isto é, os estudantes precisavam ser nivelados para acompanhar o aprendizado de análise. A criação desse novo curso foi atribuída ao matemático e físico francês Jean-Baptiste Joseph Fourier, que teria um papel fundamental na discussão sobre o conceito de função.
Os trabalhos de Fourier sobre a teoria da propagação do calor datam dos primeiros anos do século XIX e estão associados à redefinição do conceito de função. Tratamos de seus métodos ainda neste capítulo para enfatizar que seus estudos partiam de um problema físico: saber como o calor se propaga em uma massa sólida, dadas certas condições iniciais. Quando o calor é desigualmente distribuído em diferentes pontos da massa sólida, ele tende a se colocar em equilíbrio e passa lentamente das partes mais quentes às menos quentes, como se estivesse em um tubo que atravessa perpendicularmente as curvas de mesma temperatura sobre a superfície sólida. Seguindo um raciocínio físico, ele deduzia que a difusão de calor é governada por uma equação diferencial parcial.”
“Ao fornecer a solução de um problema considerando somente um intervalo, ou definir uma função somente em um intervalo, Fourier apresentava um recurso inovador em relação à definição da função pela sua expressão analítica. Nesse caso, uma função era determinada automaticamente se a expressão analítica estivesse bem-estabelecida. Não era necessário prestar atenção ao domínio de definição da função; aliás, sequer existia essa noção de domínio. Essa e outras definições desse tipo, que nos são bastante familiares, começaram a aparecer nesse momento, mas só se desenvolverão com o estudo dos conjuntos numéricos.”
“Até os anos 1820, as séries de Fourier eram vistas com desconfiança, pois contradiziam a concepção aceita sobre a natureza das funções. A razão dessa desconfiança não advinha tanto do fato de ele enxergar a soma de uma série de potências como uma função – isso estava de acordo com os padrões da época – e sim de afirmar que uma função qualquer pode ser representada por uma série trigonométrica. Ora, isso implicava dizer que a função era algo mais do que a sua representação. Ou seja, implicava dizer que existe um objeto que é a função e que esse objeto pode ser representado por uma série. A expressão analítica, nesse caso, não seria a função.”
“suas soluções representavam fenômenos físicos com precisão e não podiam simplesmente ser descartadas. Se o método funcionava, era interessante investigar por quê.
Para além de exemplos específicos, Fourier não demonstrou realmente que uma função qualquer pode ser representada por uma série trigonométrica em um intervalo. Ou seja, mesmo em um intervalo restrito, não havia uma demonstração satisfatória de que essa série convergisse para a função. Quem daria continuidade ao trabalho de Fourier nessa direção seria o matemático alemão Gustav Lejeune Dirichlet, em 1829”
“No meio francês, os matemáticos, sobretudo Lagrange, estavam convencidos de que as séries de Fourier não convergiam. Para tentar persuadi-los, Fourier fez alguns experimentos comparando as predições de seu modelo matemático com fenômenos efetivamente observados.
O problema do fluxo de calor interessava a muitos pesquisadores da época, e, em 1811, houve um concurso da Academia para escolher a melhor explicação sobre o tema. Fourier ganhou o prêmio e começou a escrever um livro com o fim de difundir suas idéias. A obra Théorie analytique de la chaleur (Teoria analítica do calor) foi publicada em 1822 e Fourier passou a ocupar um lugar de destaque na cena matemática francesa. Nesse livro encontramos uma definição mais geral do termo ‘função’, freqüentemente citada nos textos sobre a história dessa noção:
Em geral, a função fx representa uma sucessão de valores, ou ordenadas, cada um dos quais é arbitrário. Uma infinidade de valores sendo atribuídos à abscissa x, existe um número igual de ordenadas fx. Todas têm valores numéricos atuais, ou positivos, ou negativos, ou nulos. Não se supõe que essas ordenadas estejam sujeitas a uma lei comum; elas se sucedem uma à outra de um modo qualquer, e cada uma delas é dada como se fosse uma única quantidade.”
“pode acontecer, em tese, de a função ter valores infinitos, mas se os valores da abscissa estiverem compreendidos entre limites bem-determinados, é impossível que ‘uma questão natural conduza a supor que a função fx se torne infinita’.
Fourier não subscrevia a profissão de fé dos matemáticos do século XVIII de que uma função se identificava à sua expressão analítica. Para ele, 2 funções dadas por expressões analíticas diferentes podem coincidir em um intervalo sem coincidir fora dele. Vemos, assim, que sua definição de função é mais geral do que a usada anteriormente, sobretudo por não desconsiderar a lei que governa o modo como a ordenada depende da abscissa.”
“Portanto, o termo ‘atual’, usualmente esquecido nas histórias sobre a noção de função, é essencial na definição de Fourier, que não considerou, efetivamente, funções arbitrárias.(*) Vale lembrar que essa definição não possui nenhum destaque no texto; surge embaralhada no meio de resultados físicos sobre a propagação do calor que envolvem a integração de equações diferenciais.
(*) As funções empregadas por ele são as que diríamos, hoje, ‘contínuas por partes’.
A teoria de Fourier superará as desconfianças e ganhará grande destaque no século XIX. O problema da convergência das séries trabalhado por ele será abordado por Cauchy em 1826. Esse trabalho continha algumas falhas, o que levou Dirichlet a escrever um artigo sobre o tema 3 anos depois com uma boa demonstração, segundo seus critérios, da convergência das séries de Fourier.
Os problemas físicos tratados geometricamente por meio do cálculo no final do século XVII continuaram a ocupar um papel de destaque no século seguinte. A competição entre os métodos de integração de Newton e Leibniz teve grande impacto na Academia de Ciências de Paris a partir de meados dos anos 1730, graças, principalmente, ao estímulo de Pierre-Louis Maupertuis. Diante da urgência de resolver problemas específicos de natureza físico-matemática, ficava em segundo plano a discussão filosófica, como a que existia entre cartesianos e newtonianos. Assim, a teoria newtoniana sobre a forma da Terra ganhou popularidade na França nos anos 1730 e as discussões a esse respeito moldaram a física matemática francesa. Ao mesmo tempo, os debates sobre o princípio da mínima ação, influenciados por Leibniz, eram intensos nos anos 1730-40, envolvendo contribuições de Maupertuis e d’Alembert.
Ainda que tenha sido escrito anteriormente em latim, o Método das fluxões e séries infinitas, de Newton, foi publicado em inglês em 1736 e traduzido por Buffon para o francês em 1740. Nesse momento, o pensamento newtoniano tornou-se bastante popular na França. A visão sobre a física implícita nessa obra, bem como nos trabalhos sobre o cálculo infinitesimal, implicava que as variáveis e os coeficientes descritos pelas funções se relacionavam de modo vago com a realidade das leis da natureza. Para Buffon, o uso da análise tornava os princípios físicos opacos ao entendimento. Uma equação como a da queda livre, que associa a posição de um corpo ao tempo transcorrido na queda, era uma imagem direta da lei natural que rege esse fenômeno, ou seja, exprimia sua causa física. No entanto, as séries infinitas, principal ferramenta do cálculo, não podiam ser compreendidas como uma soma de causas físicas, o que foi criticado por Buffon em um intenso debate com Clairaut. Para mais detalhes, ver J. Dhombres, ‘The mathematics implied in the laws of nature and realism, or the role of functions around 1750’.
Motivada pelo pensamento newtoniano, como também por pesquisas francesas, uma comunidade singular de física matemática começou a se desenvolver na França nessa época. Outras influências, como a de Euler, a partir dos 1740, além da invasão de farta literatura de outros países, ajudaram a formatar o seu estilo. Esse processo culminou com o papel preponderante que Laplace adquiriu a partir dos anos 1770, somado à transferência de Lagrange de Berlim para Paris, em 1787. Paris se tornava, assim, o centro da física matemática européia. Inicialmente, as pesquisas continuaram a versar sobre os mesmos problemas tratados anteriormente: a teoria sobre a forma da Terra; questões ligadas à estabilidade do Sistema Solar, entre elas o dos três corpos e a teoria da Lua; além de problemas de dinâmica, como o estudo do movimento, da conservação da energia e do princípio de mínima ação.”
“A física precisava lidar com séries infinitas, pois os fenômenos eram descritos por equações diferenciais e as soluções dessas equações eram dadas por séries infinitas. Uma função era escrita como uma série e não interessava explicar sua forma em termos de causas físicas, já que ela permitia descrever a evolução do fenômeno. O poder da álgebra fazia com que fosse menos necessário para uma fórmula representar a realidade do que possibilitar um cálculo.
Aos poucos, percebeu-se que vários fenômenos físicos podiam ser descritos por equações diferenciais análogas, e o problema de deduzir e resolver as equações que descrevem os fenômenos tomou o lugar da explicação física. Na segunda metade do século XVIII, a elaboração da mecânica analítica transformou a física matemática de um saber geométrico em um saber analítico. Para Lagrange, por exemplo, a mecânica era um ramo da análise. Isso não aconteceu com o estudo dos fenômenos naturais em geral – muitos continuaram a possuir métodos próprios e a investigar os princípios por meio de ferramentas matemáticas variadas.”
“Para que a atração pudesse ser concebida como uma força, seria necessário identificar os traços manifestos que a exprimem. Se afirmamos que um planeta gira em torno do Sol graças a uma força, precisamos mostrar como o Sol se liga a esse planeta, do contrário, supõe-se que deva ser dotado de um motor. Newton hesitava sobre a resposta a essa questão. Sua obra mais importante, Princípios matemáticos da filosofia natural, publicada originalmente em 1687, ganhou um acréscimo em sua 2ª edição, de 1713, denominado Escólio Geral, no qual encontramos um comentário que busca responder às críticas recebidas:
Mas até aqui não fui capaz de descobrir a causa dessas propriedades da gravidade a partir dos fenômenos, [e ninguém jamais irá!] e não construo nenhuma hipótese; pois tudo que não é deduzido dos fenômenos deve ser chamado uma hipótese; e as hipóteses, quer metafísicas ou físicas, quer de qualidades ocultas ou mecânicas, não têm lugar na filosofia experimental.”
“hypotesis non fingo (…) Para se livrar do problema proposto por Leibniz, Newton argumentou que não vale a pena pesquisar a causa da gravitação.” “Entendida como uma lei, ela pode ajudar a descrever os fenômenos, e isso basta, ou seja, não precisamos nos preocupar com as questões relativas à causa da gravitação. Essa resposta, aperfeiçoada no século XVIII, exclui as questões sobre a causa e a natureza física da atração. Assim, a filosofia experimental deve tratar somente das propriedades manifestas; já as qualidades físicas podem ser negligenciadas em favor de quantidades e proporções matemáticas.”
“Foi a partir do século XVIII que a lei de atração universal passou a ser concebida como um fato científico independente de sua natureza. Esse tipo de investigação abre mão do porquê para investigar somente como os fenômenos acontecem. Koyré apresentou uma avaliação negativa dessa transformação: ‘O pensamento do século XVIII se reconcilia com o inexplicável.’” Bobão!
“Esse quadro foi estabelecido no século XVIII e as pesquisas sobre a estabilidade do Sistema Solar fornecem um exemplo perfeito desse ponto de vista. Tais estudos partiam do problema de Newton: como garantir que a atração não perturbe a trajetória dos corpos em torno do Sol? Na descrição kepleriana, a órbita de cada planeta em torno do Sol deveria ser elíptica, considerando apenas a interação entre esse planeta e o Sol. Mas, com o uso da lei de atração universal para descrever todos os movimentos do Sistema Solar, passamos a ser forçados a considerar a perturbação causada pela atração dos outros corpos. No Escólio Geral, Newton acrescentou: ‘Este magnífico sistema do Sol, planetas e cometas poderia somente proceder do conselho e domínio de um Ser inteligente e poderoso.’” Shut up, fool!
“Contra essa necessidade da intervenção de um Deus que salvaguardasse a estabilidade do Sistema Solar se dirigiram inúmeras críticas, a começar por Leibniz, que acusou o Deus de Newton de funcionar como um relojoeiro responsável por recolocar regularmente a máquina do Universo em funcionamento.”
“Laplace lamentava que Newton não tivesse enxergado todo o poder de suas leis, e isso se devia à utilização da geometria sintética. Para devolver ao sistema newtoniano sua vocação explicativa, era fundamental traduzi-lo por meio das ferramentas da análise matemática, ‘esse maravilhoso instrumento sem o qual seria impossível penetrar em um mecanismo tão complicado em seus efeitos quanto em suas causas’ (Laplace, Exposition du système du monde). A formulação analítica do problema da estabilidade e sua demonstração eram elementos cruciais para atestar a legitimidade da concepção do Universo conforme descrito por leis matemáticas. Lagrange e Laplace exprimiram esse problema em termos de séries infinitas obtidas como solução de equações diferenciais.”
“A síntese geométrica tem a propriedade de não deixar que se perca de vista o seu objeto e de clarear todo o caminho que conduz dos primeiros axiomas às suas últimas consequências; ao passo que a análise algébrica nos faz logo esquecer o objeto principal para nos ocuparmos de combinações abstratas. … Tal é a fecundidade da análise; basta traduzir nessa língua universal as verdades particulares, para ver sair de suas expressões uma multidão de novas e inesperadas verdades. Nenhuma língua é tão suscetível de elegância.” L.
“Dessa forma, o critério para considerar uma explicação aceitável de um fenômeno físico (como o da gravitação) deixava de ser mecânico e passava a ser matemático. Se fosse possível obter uma formulação matemática de um fenômeno, ainda que não se soubesse sua causa física, devia se prosseguir na investigação por meio da equação.”
“Deduzindo das fórmulas as conseqüências mais sutis e mais distantes dos princípios e testando-as por meio de experimentos, pode-se verificar, realmente, se uma teoria é falsa ou verdadeira. Sendo assim, o método da ciência experimental passou a se basear na matemática e na física e a experiência adquiriu o papel de mera verificação de uma teoria, ao passo que a explicação foi identificada à fórmula matemática. Essa mudança teve conseqüências na física do século XIX, principalmente na separação da pesquisa matemática em relação aos problemas físicos que tinham exercido um papel central no desenvolvimento do cálculo infinitesimal.”
“De modo similar, essa narrativa tradicional enxerga a construção dos diferentes conjuntos numéricos a partir de extensões sucessivas: primeiro os naturais, depois os inteiros, os racionais, os reais e os complexos. Mas essa construção, embora didática, não possui fundamento histórico, além de fornecer uma imagem da evolução da matemática tal qual um edifício estruturado, erigido sobre bases sólidas. A constituição da noção de rigor, ora vigente, está ligada à história da análise matemática. Na maioria dos livros que tratam do tema, as práticas dos analistas do século XVIII aparecem como inconsistentes em comparação com a análise moderna, desenvolvida a partir de Cauchy. Dentro desse espírito, chega-se a afirmar que, na virada do século XVIII para o XIX, os matemáticos começaram a se preocupar com a inconsistência dos conceitos e provas de amplos ramos da análise e resolveram colocar ordem no caos. (…) Essa mistificação gera sérias conseqüências no modo como noções básicas da matemática nos são apresentadas até hoje – caso da definição de funções e de números por meio do conceito de conjunto.”
[+]
Cohen, The Scientific Revolution: a Historiographical Inquiry
Corry, The history of modern mathematics: writing and rewriting
Cuomo, Pappus of Alexandria and the Mathematics of Late Antiquity
Fowler, The Mathematics of Plato’s Academy: A New Reconstruction
Gonçalves, A história da história da matemática antiga
Høyrup, ‘The formation of a myth: Greek mathematics – our mathematics’ (art.)
Knorr (o professor que dá um caldo, cof, cof…), The Evolution of the Euclidean Elements, 1975 (tese de doutoramento).
Netz, The history of early mathematics: ways of re-writing
Nobre, Introdução à história da história da matemática: das origens ao século XVIII
Rashed, Al-Khwarizmi: Le commencement de l’algèbre
Struik, The historiography of mathematics from Proklos to Cantor